概要

　数学では「空間」という言葉が頻繁に現れます。どのような空間をどのような意味で調べるかによって様々な分野に分かれます。具体例をあげましょう。

　たとえば、ドーナツの表面とコーヒーカップの表面は「本質的に同じ」空間である、と考える分野があり、それはトポロジーと呼ばれます（図1）。ここでの、本質的に同じ、は両方を粘土のようなやわらかい材質でできていると思って粘土を伸ばしていくと、ドーナツの表面はコーヒーカップの表面に変身（より正確には変形）できることを意味しています。

　しかしドーナツを買うつもりで買い物に行ってコーヒーカップを買ってくる人はまずいないでしょう。それは両者の「形」が明らかに違うため、日常の感覚だとその二つは違うものだからです。より正確には、両者が鉄のような固い物質でできていると思ったら、上のような変形はできない、よって異なる、といえます。この「固い物質でできていると思ってその形を重視する幾何学の分野」をリーマン幾何学といい、私はそれを研究しています。

　リーマン幾何学で現れる空間のことをリーマン多様体と呼びます。よってコーヒーカップの表面はリーマン多様体の一例です。そしてリーマン多様体の上では、様々な微分方程式を考えることができます。微分方程式とは現象を記述する方程式だと考えてOKです。

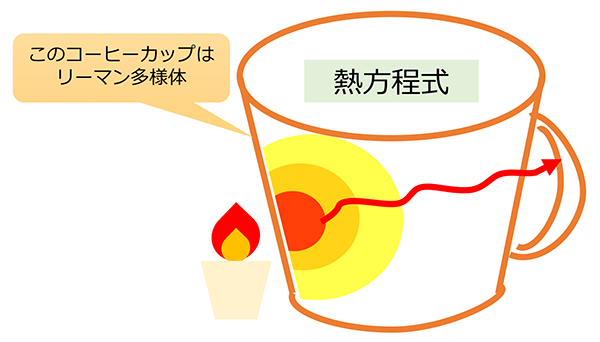
　たとえば、コーヒーカップの表面のどこか一点に熱を浴びせたとき、その熱がコーヒーカップ全体にどのように伝わるか、という問いを考えます。どこかを熱くしたとき取っ手の部分がいつ熱くなって持てなくなるか、を考えているような感じです。この問いの答えは熱方程式と呼ばれる微分方程式をコーヒーカップ上で解くと得られます。熱方程式はコーヒーカップ上に限らず全てのリーマン多様体上で考えることができ、そこでも非常に重要な方程式の一例として知られています。（図2）

　私はリーマン幾何学の中でも特に、リーマン多様体の非常に弱い変形に興味を持っています。その変形とはグロモフ・ハウスドルフ収束^（注1）と呼ばれ、空間のトポロジーが大きく変わってもよい、非常に弱い変形です。この変形を調べる分野をリーマン多様体の収束理論と呼びます。私の研究分野はまさにここです。この理論は数学の大きな未解決問題であったポアンカレ予想^（注2）の証明の中でも本質的に使われ、近年非常に注目を集めている理論です。

　リーマン幾何学に現れる空間、リーマン多様体は全てつるつるな、すなわち滑らかな空間ばかりなのですが、この収束理論では尖った、すなわち特異点もあるような空間を考えることが自然になります。ここでグロモフ・ハウスドルフ収束の例をあげましょう。

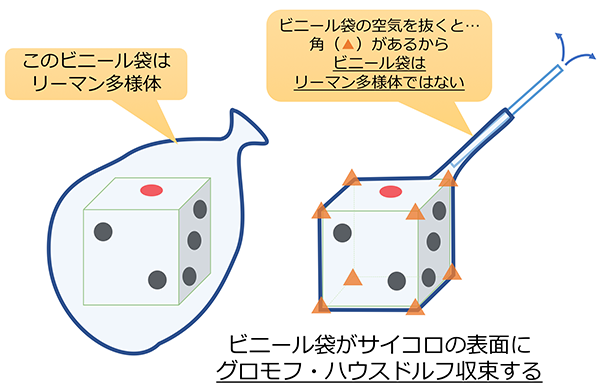
　サイコロの表面を考えます。これは角が8つあるので滑らかではありません。このサイコロをビニール袋で優しく包みます。そして中の空気を一気に抜きます。すると、ビニール袋がサイコロの表面に張り付くことが想像できると思います。張り付くまではビニール袋に角はありません。すなわちビニール袋はリーマン多様体です。ですが張り付いた先のサイコロの表面には角があるため、それはリーマン多様体ではありません。この現象をビニール袋がサイコロの表面にグロモフ・ハウスドルフ収束するといいます。この例からもリーマン多様体の極限は滑らかとは限らないことがわかります。（図3）また実は、図1の変形もグロモフ・ハウスドルフ収束と思うこともできます。

　私はこのようなグロモフ・ハウスドルフ収束のもとで、どのような微分方程式がおもしろく振舞うか、という問いに興味を持って調べています。実はその際、最も重要な方程式は、上で述べた熱方程式です。熱方程式をサイコロの表面のような角がある空間でも考えることがポイントです。それらを調べることで他の、非常に複雑な微分方程式も調べることができる、ということがわかってきました。

研究内容

　どんなリーマン多様体の上にもテンソル^（注3）と呼ばれる量が定義できます。これはリーマン多様体の各点の上に行列を定めるようなものです。特に重要なものとして、どんなリーマン多様体にもリーマン計量と呼ばれる自然なテンソルが唯一つあります。これらはリーマン多様体のグロモフ・ハウスドルフ極限空間として現れる、（特異点があるかもしれない）空間でも同様であることが知られています。

　例えば上で議論された、極限空間の一例であるサイコロの表面のリーマン計量とは、サイコロの表面の各点に2×2単位行列を置くことに他なりません。

　私はリーマン多様体の列が、（特異点があるかもしれない）ある空間にグロモフ・ハウスドルフ収束している状況を考え、その各リーマン多様体上にテンソルを一つずつ取って、さらに極限空間上にもテンソルを一つ取って、それらテンソルの収束の概念を定義しました。

　例えば、ビニール袋がサイコロの表面にグロモフ・ハウスドルフ収束している例を思い出してください。この例ではビニール袋のリーマン計量が、サイコロの表面のリーマン計量（各点に2×2単位行列が置かれているもの）に収束していることが示せます。

　このテンソルの収束の概念とその基本的性質は応用が広く、これを用いて、等周問題、山辺の方程式、ホッジラプラシアン、pラプラシアンといった微分方程式と、グロモフ・ハウスドルフ収束との密接な関係を与えることができました。それらを応用してリーマン多様体自身への応用も見つかりました。

　このような研究の方法はリーマン多様体の社会学と呼ばれるもので、個々のリーマン多様体を調べるのではなく、その全体を調べることでなされるものです。その社会をグロモフ・ハウスドルフ収束理論の道具を用いて調べる、この方針でまだまだ研究をやっていきたいと思っています。

発表雑誌

Shouhei Honda, Ricci curvature and convergence of Lipschitz functions, Communications in Analysis and Geometry, 19 (2011), no.1, 79-158.
Shouhei Honda, A weakly second-order differential structure on rectifiable metric measure spaces, Geometry & Topology, 18 (2014), no.2, 633-668.
Shouhei Honda, Ricci curvature and L^p-convergence, Journal fur die reine und angewandte Mathematik, 705 (2015), 85-154.
Shouhei Honda, Spectral convergence under bounded Ricci curvature, Journal of Functional Analysis, 273 (2017), no.5, 1577-1662.
Shouhei Honda, Elliptic PDEs on compact Ricci limit spaces and applications, to appear in Memoirs of the American Mathematical Society.

用語解説

(注1) グロモフ・ハウスドルフ収束
ハウスドルフ距離という古典的に知られていた距離があるが、それを内在的にしたものとしてグロモフが定義した概念。最近ではこの収束理論を本質的に使って、ケーラー・アインシュタイン計量の存在問題に関する大きな未解決問題も解かれた。

(注2) ポアンカレ予想
1904年にポアンカレによって予想され、2000年代に入ってペレルマンによって解かれた、クレイ数学研究所が提出したミレニアム問題の一つ。この解決によってペレルマンに、フィールズ賞と約一億円の賞金が与えられることになったが、どちらも辞退した。

(注3) テンソル
行列の一般化。例えば数を長方形の形に並べたものが行列であるが、直方体の形に並べるとそれはテンソルとみなせる。

問い合わせ先

東北大学大学院理学研究科 数学専攻
准教授　本多 正平（ほんだ しょうへい）
E-mail：shonda[at]m.tohoku.ac.jp
＊[at]を@に置き換えてください

Posted on：2017年11月15日