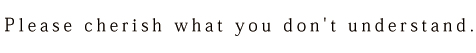I study the behavior of singular solutions (solutions that are smooth except for one point and diverge at that point) of nonlinear elliptic partial differential equations. It has its roots in a field called potential theory, and one of its origins is the law of universal gravitation. Let me explain a little more. (a) If we consider a state in which mass is virtually concentrated at one point, the scalar potential of universal gravitation produced by that point (point mass) is a harmonic function in the punctured domain except the point. (b) Furthermore, it can be mathematically proven that the universal gravitation force created by a spherical matter with a constant density distribution is the same as the universal gravitation force when a mass point is placed at the center. From (a) and (b) above, if the density distribution is constant and spherically symmetric, one can assume that the matter is a point mass, therefore one can learn a lot by studying the properties of harmonic functions in punctured domains.
Various studies have been derived from here, and my research corresponds to potential analysis with nonlinear reaction terms. Currently, I'm studying a method to simply analyze nonlinear problems by classifying nonlinearities and reducing nonlinear problems to model equations with some good properties.

To be honest, there wasn't much that could be said to be the reason, but I guess that the following question I had when I was an undergraduate might be the reason, that is: “Among real-valued functions of which the integral is bounded near the origin, what is the function with the fastest divergence at the origin?''
From this question, several chains of questions arise, like, what is an integrable function? What is the delta function? What is singularity? How about if there is an external force? How about if there is a nonlinear effect? What is the structure for classifying nonlinear effects? I feel that my current research has come about through these questions intertwining with potential theory.

(a)Please cherish what you don't understand.
(b)Please keep in your mind that all understanding is a temporal one.
Because, once you think that you totally understand something, the path to deeper understanding will be closed.