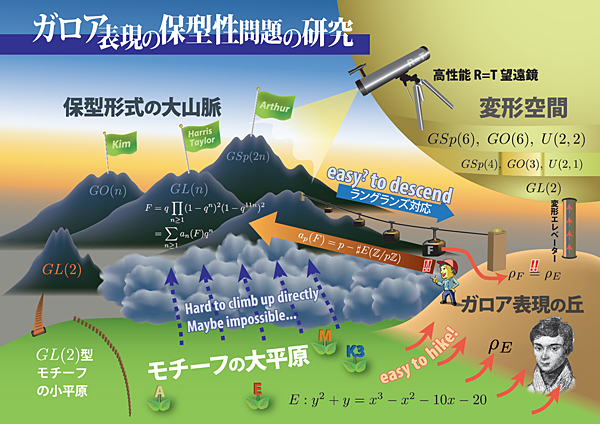
概要

　数学は数式の神秘さを問う学問と勘違いされる方も多い様ですが、それだけではなく、様々な起源をもつ数学的対象が思いもよらない形で結びつくことで豊かな土壌をうみだす学問とも言えます。今回の研究はガロア表現^（注１）の保型性問題についてです。この問題は、保型形式^（注２）と呼ばれる解析的対象とガロア表現と呼ばれる代数的対象の間に成立すると予想されている神秘的な対応に関連する問題です。たとえば、1995年頃にワイルズによって証明された、方程式xⁿ+yⁿ=zⁿ の整数解(x,y,z)には自明なものしかないという主張は、この保型性問題のある特別な場合の帰結になります^（注３）。さて、一般に保型性問題を解決するに当たって重要なことは関連する周辺分野の進展にあります。例えて言えば宇宙船を作るかのごとく様々な分野の知識が高度なレベルで要求されるのです。今回、焦点を当てるのはセール予想というある種のガロア表現の保型性を問う問題です。それを解決するためには、幾つもの課題を克服しなければなりません。ここ数年の研究においてGSp₄^（注４）の場合にセール予想^（注５）に関連する重さ還元定理というものを証明することができました。この結果はセール予想の解決に向けて大きく寄与することが期待されます。
　本研究は、JSPS科研費 15K04787「基盤研究(C) 一般」の助成を受けたものです。

研究内容

　重さ還元定理はガロア表現の局所的な性質に関連するものでその性質が予想として対応する保型形式の「重さ」と呼ばれるパラメータを記述する際、「それをどのように行えばよいか？」という事に対し道標を与えてくれるものと期待されています。本研究では代数群GSp₄上の保型形式を扱いました。重さ還元定理を証明するためのアイデアは正標数体上の幾何学を援用することでした。保型形式と呼ばれるものは解析的な対象ですが、それを代数化し、別の世界の対象へ舞台を移すことができます。その世界ではもとの世界にはない不思議な現象が幾つもありそれを援用して、その世界で一度重さを「還元」します。ところが話はそう上手く行くわけではなく、世界を変えたとき、元に戻るのはそう容易ではないということです。そこで、元の世界に戻るために各中継地点に幾つかの基準を設ける必要があったのですが、その役割を果たしたのが部分ハッセ不変量^（注６）と保型的コホモロジーの消滅定理^（注７）でした。また、ガウスーマニン接続と呼ばれる微分形式と保型形式を動かすことで、第2基本重さの部分をできる限り小さくできることも分かりました。
　この重さ還元定理とテータサイクルと呼ばれるものを用いてセール予想に関連するセール重さを「どのように定義するか？」ということと重さ還元定理の改良が当面の課題で、この部分が進展すればGSp₄の場合のセール予想の解決に大きく前進するものと思われます。

発表雑誌

Takuya Yamauchi, The weight reduction of mod p Siegel modular forms for GSp4, http://arxiv.org/abs/1410.7894, submitted for the publication.

用語解説

（注1）ガロア表現
有理数体の絶対ガロア群の線形表現のこと。係数体は主に、複素数体、p進体の拡大体、および、有限体を想定している。

（注2）保型形式
極めて高い対称性を持った複素数値関数で良い性質を満たすもの。

（注3）フェルマーの最終定理と呼ばれ300年もの間未解決でした。

（注4）GSp₄
半単純ランクが2の一般斜交群。

（注5）セール予想
有限体を係数体にもつガロア表現の保型性問題に関する予想。

（注6）部分ハッセ不変量
Ekedahl-Oort 階層上に定まる正則関数。

（注7）保型的コホモロジーの消滅定理
保型的ベクトル束のある次数のコホモロジーが自明になるという主張の定理。

お問い合わせ先

東北大学大学院理学研究科
数学専攻
准教授 山内卓也（やまうちたくや）
E-mail：yamauchi[at]math.tohoku.ac.jp

＊[at]を@に置き換えてください

Posted on：2016年9月20日