図１：カーボンナノチューブの鏡像異性体（a）、分子の鏡像異性体（b）

概要

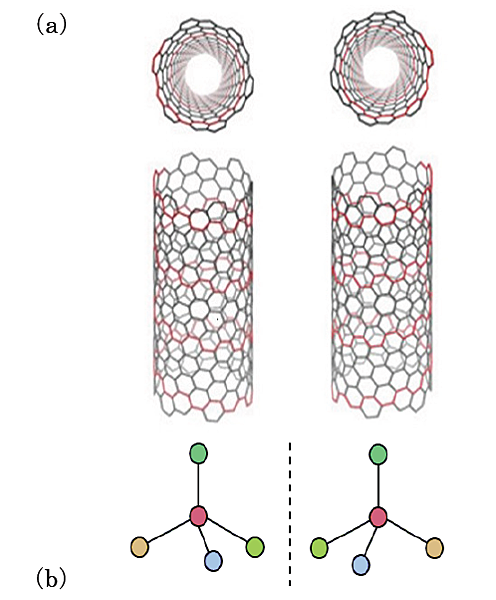
　東北大学の齋藤理一郎教授と大学院生の佐藤直道、辰巳由樹は、産業技術研究所片浦弘道首席研究員、魏小均特別研究員らとともに、カーボンナノチューブ^（注１）の右巻きと左巻きの立体構造を区別する、円偏光二色性^（注２）の新たな理論を作り、実験で観測された複数のナノチューブ構造の円偏光二色性スペクトルを説明しました。
　本研究は、文部科学省の新学術領域研究「原子層科学」（領域代表：齋藤理一郎）、基盤研究（S）（研究代表者：片浦弘道）、基盤研究（B）（研究代表者：齋藤理一郎）の支援を受けて行われたもので、Nature Communications　に2016年10月5日（DOI: 10.1038/ ncomms12899）に発表されました。

研究の背景

　化学の世界では、分子の中には鏡像異性体（分子の鏡像が元の分子構造と同じにならない異性体の組）^（注３）があることが知られています。鏡像異性体に光を当てると、符号の異なる旋光性（光の偏光面の回転）が発生しそれによって、右巻きと左巻きの分子を区別できます。地球のすべての生物中の分子は、左旋光性を持ち、生物の食物も左旋光性を持ちます。したがって人工的に合成した分子が右旋光性を持つと生体適合性が無く、時には有害にもなります。エネルギー的にまったく同じ鏡像異性体の片方だけを合成することは、化学の大きな課題の一つです。例えば、2001年に野依良次先生は、特殊な触媒を用いて鏡像異性体を作り分けた業績でノーベル化学賞を受賞されています。
　グラファイトの１原子層（グラフェン）を丸めた円筒形物質であるカーボンナノチューブ立体構造も、らせん構造をとり、右巻きと左巻きがあります。しかし合成では右巻きと左巻きが同じ確率で合成され分離することは不可能であると考えられていました。
　近年片浦や世界の研究者はそれぞれ独自の方法を用いて、特定の立体構造を分離する技術を確立し、さらに右巻きと左巻きを分離することに成功しました。そのアイデアは、ナノチューブを生体由来のゲル（寒天）に吸着させると、右巻きか左巻きのどちらかがより吸着しやすいという性質を利用しています。このような技術が確立されると、どれぐらい正確に鏡像異性体を分離できたのかという評価手法の確立が必要になります。今回の論文では、界面活性剤を使ってナノチューブを溶液中に溶かし、円偏光二色性の実験を行いました。そして、この円偏光二色性の実験を説明する理論が必要になってきました。

研究の内容

　東北大学のグループは、この円偏光二色性の理論的な計算を行いました。従来の化学では、分子における円偏光二色性の大きさは、「電気双極子モーメント」と「磁気双極子モーメント」の積で与えられるという理論があり、広く分子の計算で使われています。ところが、ナノチューブは、電子状態にある特殊な対称性があり、円偏光二色性の計算をすると（１）右円偏光のK点付近の光吸収と（２）左円偏光のK'点付近の光吸収強度が等しくなって、光吸収の差が０になってしまいました（ここで、K点、K'点とはグラフェンで光吸収が起こる２つの場所^(注４)を示す名前です。）これでは、実験結果を再現できません。つまり従来化学で良く用いられている円偏光二色性の理論では、ナノチューブの円偏光二色性を説明できませんでした。そこで従来の理論で使われていた「ナノチューブの大きさが光の波長に比べて無視できるほど小さい」という近似を使わずに、新たな理論を作り円偏光二色性の式を提案し（これについては現在論文を作成中）、数値的に計算した結果と実験結果と比べたところ、複数の立体構造のナノチューブの円偏光二色性の複数ある実験事実の特徴をすべて再現することができました。

今後の展開

　ナノチューブを生体に応用する場合には、この分離技術と円偏光二色性の理論によって、鏡像異性体の純度を評価することが可能になります。この技術は、サンプルとして分離ナノチューブを提供するときの品質の基本的な評価条件になります。理論的には、最近注目されているカイラルな固体に対する、円偏光に対する光物性を今後開拓していくことが考えられます。

参考図

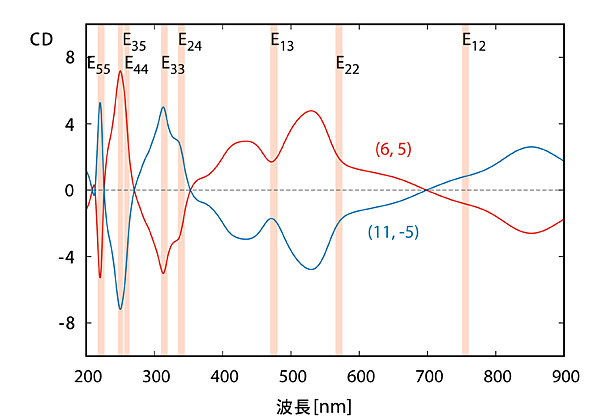図2：円偏光二色性（CD）の値を波長でグラフにしたもの。鏡像異性体の関係がある、(6，5)ナノチューブと(11、-5)ナノチューブの符号が逆になっています。また波長の関数として、CDの符号が変わること、特定のエネルギーでピークを持つことなどの特徴は、10組以上のナノチューブ実験結果にも表れ、実験をよく説明しました。

用語解説

（注1）カーボンナノチューブ
グラファイトの１原子層（グラフェン）を丸めた円筒形物質。（「フラーレン・ナノチューブ・グラフェンの科学」、共立出版、齋藤理一郎著）

（注2）円偏光二色性
円偏光とは電磁波の電場のベクトルが進行方向に向かって、右回りか左回りのどちらかに回転するような偏光の状態のこと。円偏光二色性とは右円偏光と左円偏光の光の光吸収強度の差で定義される。

（注3）鏡像異性体
分子の鏡像が元の分子構造と同じにならない異性体の組。

（注4）ここでいう場所は、物理の言葉では波数空間での場所であり、特定の波数を示しています。結晶中の電子の波動関数は、波数の関数で表すことができます（ブロッホの定理）。この波動関数は、波数空間で並進対称性があり、その並進対称性の最小単位をブリルアン領域と呼びます。グラフェンのブリルアン領域は６角形ですが、６角形の角の点をＫ点とＫ'点と呼びます。物理学科では、物性物理学の授業で学びます。（「基礎固体物性」齋藤理一郎著、朝倉書店）

発表雑誌

＜著者＞　X. Wei, T. Tanaka, Y. Yomogida, N. Sato, R. Saito, H. Kataura,
＜タイトル＞　Experimental determination of excitonic band structures of single-walled carbon nanotubes using circular dichroism spectra（円偏光二色性を用いた、カーボンナノチューブの励起子バンド構造の実験的決定)
＜掲載誌＞　Nature Communications. 7, 12899, (2016)　
＜DOI＞　10.1038/ ncomms12899

お問い合わせ先

東北大学大学院理学研究科
物理学専攻物性理論研究室
教授　齋藤　理一郎（さいとう　りいちろう）
電話：022-795-7754
E-mail：rsaito[at]flex.phys.tohoku.ac.jp
＊[at]を@に置き換えてください。

Posted on：2016年10月27日