お知らせ

- トップ
- お知らせ
離散群について語るとき、我々の語ること 〜群論、エルゴード理論、そして理論コンピュータ科学〜
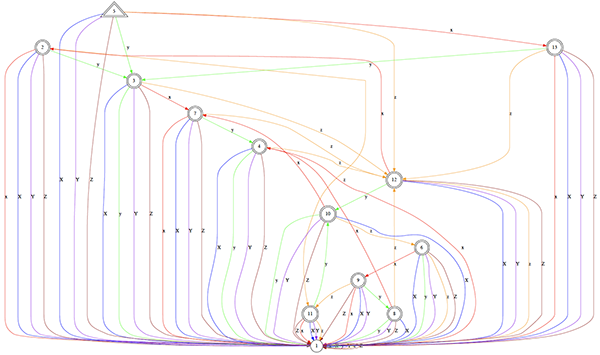
図. (4, 4, 4)三角形群のオートマチック構造(GAPにより作成)
概要
ソーンダース・マックレーンは彼の著書の一つで次のように述べています。
群論(注1)は、あのような単純な公理系から出発しながらどうしてかくも深遠なものとなるのかという疑問が湧くかもしれない。これは群の公理系のもつ若干の特色によって説明できよう。その特色はたとえば次のようにまとめられるだろう。
(a) 起源が多様であること(幾何学的変換、代数的演算)
(b) 決定的な応用をもっていること(ガロア理論、幾何学、数論)
(c) そのほかにもいろいろに応用できること(量子力学、結晶構造)
(d) その概念を生み出すもとになったものを用いて正確に表現できること。つまり、任意の抽象群(注2)は(少なくともある1つの)変換群(注3)と同型(注4)になるということ
(e) モデルの多様性:有限群(注5)には多くの種類があり、それでいてあまり多すぎないという点
(『数学--その形式と機能』彌永昌吉監修/赤尾和男・岡本周一共訳(森北出版株式会社)、p.191)
著者が「モデルの多様性」と言ったとき、念頭にあったのは主として有限群であったと思われます。それでは有限群のように、離散的(注6)であって、かつ無限の要素からなる群はどうでしょうか?
例えば、結晶構造を記述する群にこのタイプの群が現れます。このような「離散無限群」を考えるとき、「多くの種類があり、それでいてあまり多すぎない」という指摘は示唆的であると思います。それはしばしば有限群のように「原理的には」分類が可能であるような性質と、真っ向から対抗するような構造を有しているからです。
近年、離散群論の進展には目覚ましいものがあります。特に際だった特色であると筆者が思う点は、様々な分野を巻き込んで研究が展開されているところです。それは歴史的に行列からなる群が物理現象の記述に自然に現れていたのと、やや異なった仕方のように見えます。数学内部において、これまでつながっていなかった分野たちの新しい接点を見出すような発展が多く見られます。以下、この研究分野の一端を紹介したいと思います。
研究内容
有限のアルファベットからなる「語(word)」の集まりである「言語(language)」を考えます(例えば、aとbのみのアルファベットの時、語はa, b, aba, など、です。)。この言語を少し大きくすることで、次のように群の構造を入れることが出来ます。何もない「空(くう)」な語も語に付け加えます。また、アルファベットaやbに対応して、大文字のAやBを付け加えて、さらに、アルファベットの大文字と小文字が連なるaAやAa, bBやBbは空な語と考えます(キャンセルのルール)。このとき、新しい語たちを並べて繋げるという操作(「・」(ドット)で表す)に、このキャンセルを行うことで群が出来上がります。(例えばaaBとbaという語については、aaB・ba=aaaとなります。)これは、ある具体的な群の作り方の一つですが、群はいくつかの決まった公理系を満たす数学的対象として、より正確に定義されます。正確な定義を別にすれば、我々の拡張された言語である群が、有限個のアルファベットが構成する無限個の語からなることは、この例から想像できるのではないかと思います。
このような言語たちの数学的な構造を理解したいと考えます。特に、有限のアルファベットが作る無限の語からなる言語について、その仕組みを理解したい。この単純な動機は、新しい発想を呼び寄せ、多くの内容のある成果を生み出しています。ここで重要なアイデアは、この言語を幾何学の対象と見ることであったり、また、無限に長い語を、粒子のなす複雑な軌道と見たりすることであったりします。さらに、無限の語を生成するルールが有限個の規則で得られる場合には、理論コンピュータ科学における「オートマトン(注7)」によって、その仕組みを記述することができる場合があります。
例えば、平面幾何学の基本的なモデルは、平らな平面、球面(曲率が正)、双曲平面(曲率が負;いたるところ馬の鞍のように見える曲面)です。これらは空間の連続モデルとして、時空間の構造を記述する模型を研究するときに、基本的な役割を果たします。一方で、我々が相手にしたい対象は、離散的であり、その上で幾何学を考えることは、それ自体一つの問題となります。グロモフが定義した「双曲群」と呼ばれる群は、離散的な群であり、かつ負に曲がった空間の有する幾何学の性質が、離散的な形で実現されているものです。力学系では、負に曲がった空間において、粒子の等速直線運動(測地流)はカオス的に振る舞うことが知られています。双曲群を研究することで、その複雑さの性質を調べることが出来ます。また、双曲群は、言語として正規言語(normal language)、つまりある有限状態オートマトンで認識できるような群であることが知られています(サーストン、キャノンらによる)。その構造は、多くの場合、パリやロンドンの地下鉄の路線図より(はるかに)複雑です(図1)。
現在の私の研究はこれらの研究に根ざしています。発表雑誌の論文では、ヴェルシックというロシアの数学者の提起した「最大エントロピー(注8)を持つ有限生成群上のランダムウォークはいつ存在するか?」という問題について、双曲群の場合に、確率論、ポテンシャル論、エルゴード理論、そしてオートマトンに基づいた測地線のエンコーディングを援用して研究を行いました。
離散群について我々が語るとき、その語り方は実に多様です。ここで触れたのは、そのほんの一部にすぎません。
発表雑誌
Ryokichi Tanaka, Hausdorff spectrum of harmonic measure, Ergodic Theory and Dynamical Systems 37, 277-307 (2017).
用語説明
(注1) 群論
群とは数学における数ある代数構造の中で、もっとも基本的なものの1つである。群論は代数、幾何、トポロジー、解析あるいは物理学や情報理論などで出現するさまざまな群を研究する。いくつか仮想的な性質を仮定してその性質を満たす群を見つけること、あるいはそうした群は存在しないことを証明することも群論における基本的な研究方法である。
(注2) 抽象群
ある群が与えらるとき、それは往々にして生まれ持った出自が感じ取られるような記述のされ方をするが、これはその群の代数構造のみに着目したときの群のこと。
(注3) 変換群
図形や式、装飾あるいは結晶、さらに空間の対称性を記述するものとしての群のこと。
(注4) 同型
2つの群の群としての構造が一致しているとき、その2つの群は同型であるという。このとき、群としては抽象的な代数構造のみを考えている。
(注5) 有限群
要素が有限個の元からなる群のこと。例えば5個のアルファベットを入れ替える操作すべてのなす群は120個の要素からなる有限群である。
(注6) 離散的
連続的の対義語である。
(注7) オートマトン
有限個の状態の集合とその間の矢印からなる有限グラフの一種で、有限個のアルファベットからなる文字列を読み取るシステムが備わっているもの。
(注8) エントロピー
もともとは統計力学に由来する量であるが、情報理論や解析学においても基本的な量である。ここでのエントロピーは、典型的に起こりうる可能な軌道全てをコードするのに何ビット必要かを考えることで、軌道の複雑さを測っている。
問い合わせ先
東北大学大学院理学研究科 数学専攻
助教 田中 亮吉(たなか りょうきち)
電話:022-795-6401
E-mail:rtanaka[at]m.tohoku.ac.jp
*[at]を@に置き換えてください
Posted on:2019年1月30日