図1：

概要

現代数学では双対性がしばしば重要です。この聞きなれない言葉「双対性」とはなんでしょうか？　文字をみると「双対」は「二つのものAとBを対（A,B）に考えている」と連想できるかもしれません。数学におけるAとBの双対性とは、数学的対象 Aからなんらかの手続きで数学的対象Bを構成することができ, Bからもなにかの手続きでAを構成することが出来る状況をいいます。　特にAとBのデータが等価になっています。　Aにおける簡単な操作をBに移してみるとBの世界では非自明な操作になっているということもしばしば起き, 双対な対象の間を行き来することで強力な応用をもたらすことが出来るのです。

空間とその関数の間にある双対性を紹介しましょう。空間というとなんだか難しいのですが、方言みたいなもので数学では図形のことをナントカ空間とかナンチャラ多様体とかいいます。ここでは単に空間と呼ぶことにしましょう。空間の例として数直線内の0と1の間の区間を考えましょう。端の0と1も区間に含めることにします。この区間IとI上で定義された連続関数たちとの双対性を例として説明することにします。このI上で定義された関数とは、0から1までを動く変数xについての関数f(x)のことです。多項式で書くことのできる関数や三角関数など色々あります。ここではグラフが滑らかになるような関数、つまり連続関数f(x)たちを考えましょう。区間I上の連続関数たち全てのなす集合をCと書くことにします。従ってこの集合Cの要素（元）はI上の連続関数です。連続関数は足したり引いたりf(x)±g(x)、掛けたりf(x)g(x)することが出来るので, Cの要素が二つあればその足し算引き算や掛け算といった演算をすることができます。数学では、このような足し算・引き算（和・差）と掛け算（積）の二項演算の構造（代数的な構造ともいう）をもった集合を環といいます。即ちCは環になります。環C自体は連続関数たちのなす集合とその演算の構造だけでなりたっているので区間Iを忘れているように見えますが、驚くべきことに、環即ち足し算掛け算といった演算構造をもつ集合Cからイデアルなどといった代数的な概念を用いて区間Iを復元することができるのです。これが区間Iと環Cの双対性です。

数学におけるいくつもの重要な双対性はこの双対性の例の一般化とみることが出来、様々な方向に発展・進展を見せつつ研究されています。

詳細な説明

空間と環の間の双対性の哲学に沿った理論と考えられるものの中から重要な理論をいくつかあげましょう。
（１）代数方程式に関するガロア理論、代数群に関する淡中双対理論。
（２）代数幾何学におけるスキーム理論。トポス理論。
（３）クロマチック・有理ホモトピー論におけるガロア双対
（４）Koszul双対
（５）降下(descent)理論や様々なスペクトル系列、
などなど。

専門的な言葉も出てきたので少し説明します（雰囲気だけでも伝われば十分です）。空間と環の双対性を非常に明瞭に示すGelfand-Naimarkの定理があります。Grothendieckはこの双対性等に触発されて可換環という代数の双対として代数多様体^（注1）を定めることでスキーム理論を展開し、代数幾何学や数論幾何に革新的な基礎を与えました。同時にGrothendieckは同じ哲学の元, トポスという新しい空間概念に到達しました。

ガロア理論は、大まかに言えば代数方程式をそのガロア群とよばれる群^（注2）を通して理解する双対理論です。ここで代数方程式の係数が有理数とすると

[ガロア群：有理数係数の方程式]

の関係は、

[空間：関数の環]

の関係の一般化と見なすことができ, 方程式からそのガロア群（正確にはその分類空間）を定めることは上記の環Cから区間Iを構成することの類似とみなせます。淡中双対性はガロア理論の（線形な）一般化と考えられます。やや現代的な定式化では、淡中圏とよばれる対称モノイダル構造（掛け算に相当する）という構造付きでいくつかの公理をみたす圏と（プロ）代数群と呼ばれる一般化された群の間の双対性、つまり淡中双対は

[淡中圏：代数群]

の双対性を与えます。

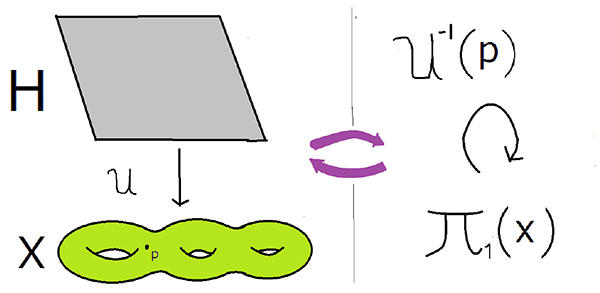
図2：被覆空間のガロア理論の例

[空間：関数の環]の双対性とその一般化の直接的なご利益はなんでしょうか。二つあげます。

（１）一見空間が見えないようなところから空間を取り出し幾何学的に考えることが出来ます。方程式から群（その分類空間）を取り出したのはその例とみなせます。

（２）"関数のなす環"は足し算や掛け算からなる環とよばれる代数系でしたが, 環を異なるタイプの代数構造にすると新しいタイプの空間を考えていると考えることが出来ます。例えば上記のCは積＝掛け算がf(x)g(x)=g(x)f(x)だから交換可能です。当たり前ですが普通の空間上の関数はいつも積が交換可能なのです。これを交換可能でないような積をもつ非可換環にすると、それの「双対になるべき」空間は普通でない「非可換空間」と考えることができます。``非可換な''幾何学などではこのような考え方が重要になります。

上にいくつか双対性に関係する理論の例を挙げましたが、実は古典的な双対性理論では収まりきらない対象が代数幾何、トポロジー、数理物理（ミラー対称性や変形量子化など）、数論（代数的サイクル・ラングランズなど）などの様々な分野から近年いくつも現れていています。私は、そのような対象へ応用することを視座におき、一方双対性のアイデアを用いながらその拡張と応用等を目標に研究しています。近年代数幾何学がホモトピー論という「やわらかい幾何学（＝連続的に変形して同一視することのできる幾何学）」と融合して---導来代数幾何などと呼ばれ---高次圏やホモトピー論、数理物理、表現論など色々な分野と有機的につながりながらエキサイティングに発展しています。　実はこのような"ホモトピー化された代数幾何"＝導来代数幾何において双対理論はより面白く深い様相をみせるのです。 そこにおける淡中双対理論への拡張やオペラッド^（注3）で統制される様々なホモトピー代数間の双対性と代数幾何の間に関連を見出すことで新たな数学を見いだせればと思っています。

発表雑誌

Hiroshi Fukuyama and Isamu Iwanari, Monoidal infinity category of complexes from tannakian viewpoint, Mathematische Annalen 356 (2013), 519--553

Isamu Iwanari, Tannakization in derived algebraic geometry, Journal of K-theory 14 (2014), 642--700

Isamu Iwanari, Bar construction and tannakization, Publication of Research Institute of Science, 50 (2014), 515--568

Isamu Iwanari, Tannaka duality and stable infinity-categories, Journal of Topology 11 (2018) 469--526.

Isamu Iwanari, Motivic rational homotopy type, preprint available at arXiv:1707.04070

用語解説

（注1）代数多様体
（一般に多変数で連立な）代数方程式（例：x^3+y^3+z^3-xyz=0）の解のなす空間を代数多様体といい、代数幾何学と関連分野の研究対象。定義づけが長い間問題だったが、Grothendieckが彼の共同研究者らと発展させたスキーム理論が現在の標準的な基礎付けになっている。

（注2）群
数学的対象の対称性を記述する概念。ガロアにより発見された。双対性の文脈では基点付き分類空間と考えたほうがよい。　もしかするとガロアも直感的にはそのように考えていたのかもしれない。

（注3）オペラッド
複雑な演算ルールをもつ代数系を記述するときに使われる。　演算ルールの回路の記述する概念。多重ループ空間の研究から生まれた。　図１はホッホシルト（コ）ホモロジーの持つ代数構造を記述するオペラッドの絵。

問い合わせ先

東北大学大学院理学研究科数学専攻
准教授　岩成　勇（いわなり　いさむ）
E-mail：isamu.iwanari.a2[at]tohoku.ac.jp
＊[at]を@に置き換えてください

Posted on：2019年11月25日