この文章は私の最近の研究成果を紹介することが目的です．以前同じくここで書いた次の文章があります：

その続き(+α) の気持ちで書いてみたいと思います．

タイトルには2つの重要な用語があります．それは空間と微分積分です．そこでまずはこれらの用語の説明から始めたいと思います．まずは空間から．空間とは何でしょうか．この問いにはいくつかの答え方があります．ここでは，図形Xと，その上のどんな2点p, q に対してもpとqの間の距離d_X(p, q) が定まっているような状況を指すこととしましょう．そのような空間X を調べることをX の幾何学といいます．例えば平面R² を考えてみましょう．平面は2つの実数x₁, x₂ を並べた(x₁, x₂) の集まりと思ってもらってOKです．平面は空間の例です．

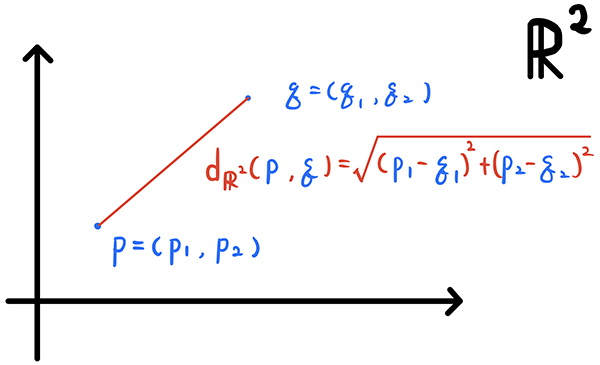
この平面R²の幾何学はユークリッド幾何学と呼ばれて，中学校でその初歩を学んだことがあるかと思います．これは字のごとく平らな空間であり，曲率が0の空間とも呼ばれます．ここで曲率という用語がでてきました．この曲率は後でもう少し詳しく説明を与えますが，ここでは三角形の内角の和と関係があるとだけ述べておくことにしましょう．

次に球面S² を考えます．それは地球の表面と考えてOK です．この地球上の2点p, q の間の距離d_S²(p, q) は地球の大円（例えば赤道や，もしくは北極と南極を結ぶ自然な弧の1 つなど) の自然な一部の長さで与えられるとします．

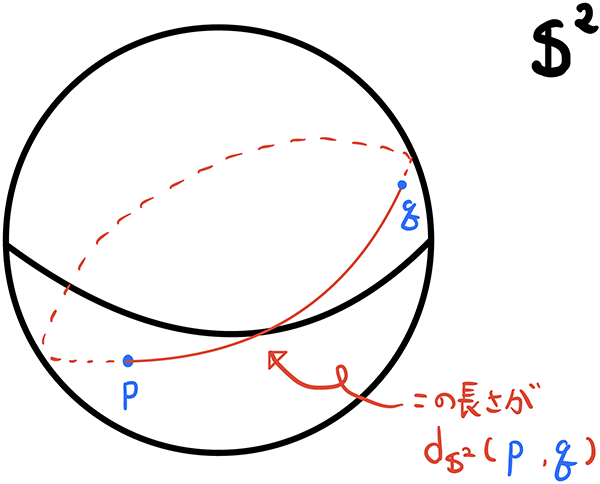
この球面は直感的にも明らかなように，平らではありません．より正確には曲率が正の空間と呼ばれます．またここで曲率という言葉がでてきました．曲率が0とか正とか，いったいそれはどういうことを表現しているのでしょうか．

先にも述べました通り，曲率を三角形の内角の和を使って説明しましょう．平面ではどんな三角形の内角の和も，もちろん180度になりますね．しかし球面だと実は180度より大きくなります．

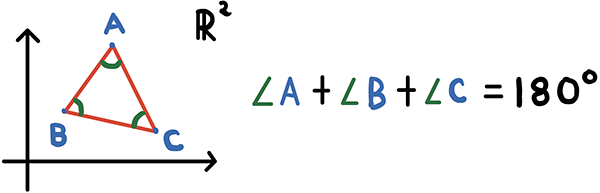
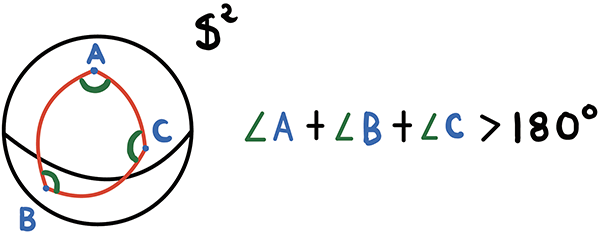
実は考えている図形X で，どんな(より正確には，小さい) 三角形を書いたとしても，その内角の和が180度となるとき平坦もしくは0曲率といって，内角の和が180度より常に大きくなるなら正曲率といいます．そしてもちろん内角の和が180度より小さくなるときを負曲率と呼びます．負曲率の例はあげていませんでしたが，馬の鞍のような形がその例になります．

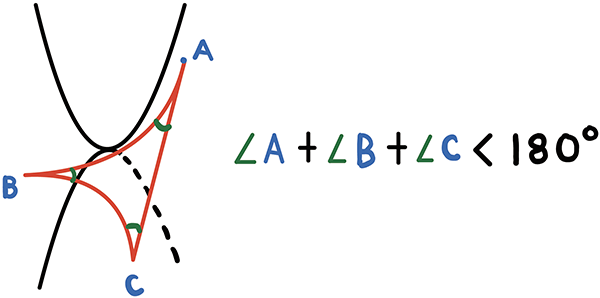
このような曲率の考え方は断面曲率と呼ばれるものになっています．私の研究ではそれより弱い，リッチ曲率と呼ばれる概念を主に扱っています．それは粗くいって，まず，いくつかの三角形をとり，それらの内角の和の相加平均をとって，それと180度を比べる概念です．このリッチ曲率は例えば相対論とも深い関係があることが知られています．

空間の説明はこれくらいにして，そろそろ微分積分の話題に移ってみましょう．
微分積分というと次の公式を思い出す方が多いかと思います：

ここでy = F(x) はその微分がy = f(x) となる関数，すなわちF'(x) = f(x) を満たす関数です．この公式(0.1) は微分積分学の基本定理とも呼ばれます．基本定理と呼ばれるだけあって，この公式が重要なことをご存じな方は多いでしょう．

実際これを使うと幾何学的な様々な量，円の面積や球の体積などを求めることができるようになります．例えば次の式(0.2) は半径がr の円の面積がπr² を表している公式になっています：

微分積分学の基本定理(0.1) を用いると，次の発散公式と呼ばれる公式が成り立つことがすぐにわかります：

ただしy = f(x) は[a, b] の境界の周りでは0とします．このg"はgを2度微分した関数で，gのラプラシアンとも呼ばれ，Δg(x) とも書かれます．(0.3) も名前がついているだけあって，重要な公式として知られていて，物理的には電磁気学の言葉を使って説明を与えることもできます．数学的には[a, b] の境界の周りでは0となっている関数に対する(0.1) の一般化とみなすこともできます．

ここで以上の式の見方を変えてみます．多くの方は(0.1) の左辺を

関数y = f(x) をaからbまで積分した数

と呼ぶでしょう．これを

関数y = f(x) を区間[a, b] で積分した数

と読み替えて，その読み替えの気持ちを汲んで

という(左辺の) 記号を導入することにします．

ここまでは1次元の話でしたが，これを高次元化することができます．話を簡単にするために平面R²を考えましょう．ここで定義された関数y = f(x₁, x₂) を平面内の三角形ΔABC上で積分する：

ということは意味があって，重積分と呼ばれます（大学初年度で学びます)．この状況でも微分積分学の基本定理および発散定理は成り立ちます．ここではその後者を三角形と絡めて紹介することにしましょう．

関数y = f(x₁, x₂)が三角形ΔABCの境界(すなわち辺) の周りで0としたときに，次が成り立ちます：

ここで∇fはfの勾配ベクトル場と呼ばれるもので，偏微分係数を単に並べて定義される，関数y = f(x₁, x₂)の1度目の微分を支配するベクトルのことです：

また，それらの内積＜∇f，∇g＞, およびgのラプラシアンΔg は次のようにして定義されます：

ここで，関数y = g(x₁, x₂) の2度目の微分を支配する行列，ヘッシアン：

の対角成分の和(トレースといいます) がgのラプラシアンに他ならないことを注意しておきます．

このような微分積分学の基本定理および発散公式は平面R²に限らず，高次元の，曲がった，角のない空間Mⁿでも同様に成り立つことが知られています．ここでnはその空間の次元を表していて，そのような空間Mⁿを調べることをリーマン幾何学といいます．平面がその典型例であったことを思い出すと，ユークリッド幾何学はリーマン幾何学の一部とみなせることになります．

空間Mⁿにおける微分積分学の基本定理および発散公式のよく知られた証明方法は，∇gを考えている空間の上の風だと思って，その風に乗ってその空間上を移動することを考えるものです．ここでもやはりgのラプラシアンΔgとはgのヘッシアンのトレースとして定義されるものです．

私はリーマン幾何学を超えて，角があるかもしれない空間X上の微分積分を通してXを調べるという幾何学をやっています．

空間Xで微分積分を行うという意味をはっきりさせておきましょう．まずその空間Xを測る測り方m(正確には測度と呼ばれます）を1つ固定します．そして，その測り方mに沿ってX上の関数y = f(x)を積分することを考えます：

これは実際に可能で，測度論と呼ばれる分野がそれを可能にしてくれます．粗く述べますと，測度mとは，曲線cに対するその長さL(c)，曲面Sに対するその面積A(S)，立体Pに対するその体積V (P)といった概念の一般化にあたるものです．

考えている空間に応じて自然な測度があります．例えば線分を考えるとき，その大きさを測る自然な測り方は間違いなく長さでしょう．これは1次元的な測り方と言えます．他にも，球面を考えるときには，その大きさを測る自然な方法は面積ですね．これは2次元的な測り方と言えます．

もちろん「線分の面積は？」と問うこともできますが，その答えは0になります．すなわち意味のある数がでてこなくなり，これは線分という1 次元の図形に対して面積という2次元的な測り方は自然ではない，ということを意味しています．同様に，「球面の長さは？」と問うと，その答えは無限大になります．これも2 次元の球面に対しては長さという1次元的な測り方は自然ではないことを意味しています．小学校，中学校，高校でこのような問いがまずなされてこない理由は，人は無意識に図形を自然な方法で測ってしまうからともいえるかもしれません．

この状況でも微分積分学の基本定理および発散公式

がいつ成り立つのか，という問いには意味があります．すなわち「微分積分の重要な公式はどんな空間にまで一般化されるのか」を問うということです．ここでラプラシアンΔgはやはりヘッシアンのトレースとして理解します．イタリアの数学者のグループは(0.11) が成り立つことと，測度mが自然なものであることは同値であろうと予想しました([DePhG18])．そしてこの予想を解決したことが私の最近の研究成果です([BGHZ21, H20])．

その証明はこれまでにない方法でなされました．それは熱方程式とよばれる次の偏微分方程式を用いるものです：

考えている空間Xを燃やすとその図形は灰になって燃え尽きますが，その燃え尽き方を支配する方程式が熱方程式です(上のリンクも参考にしていただければ幸いです)．

この熱方程式は先に紹介しましたリッチ曲率をみることでコントロールすることができることがわかっています．また，逆に熱方程式をみるとリッチ曲率もわかる，ということも知られています．この熱方程式とリッチ曲率の関係は，X上で物をうまく運ぶ方法を記述する理論，最適輸送理論，を介して発見されました．すなわち熱は空間の曲がり方を知っていて，曲がり方も熱を知っている，とも言えます．この熱方程式をリッチ曲率のコントロールとともに使って，考えている空間Xを無限次元の0曲率の空間に埋め込んで，平坦な空間の幾何学とXの幾何学を比較することで予想を証明することができました．風に乗って移動することで重要な公式の証明がなされていたことを思い出すと，これは驚きの証明であったといえます．

その証明における決定的なアイデアを紹介するには(もうすでに結構な文章を書いていて恐縮ですが) 残りのスペースは短すぎます．ですが実は本年度の理学部パンフレットの表紙の黒板に一番大事な計算の部分がさりげなく書かれていますので，ご興味を持たれた方はご覧になっていただければ幸いです：

東北大学理学部案内2022

今後も熱方程式を使って幾何学および解析学にまたがる数学の分野を行き来しつつ，研究を進めていきたいと思っています．

References

[BGHZ21] C. Brena, N. Gigli, S.Honda, X. Zhu: Weakly non-collapsed RCD spaces are strongly non-collapsed, arXiv:2110.02420.
[DePhG18] G. De Philippis, N. Gigli: Non-collapsed spaces with Ricci curvature bounded below, Journal de l'École polytechnique, 5 (2018), 613-650.
[H20] S. Honda: New differential operators and non-collapsed RCD spaces Geom. Topol. 24 (2020), no. 4, 2127-2148.

問い合わせ先

東北大学大学院理学研究科 数学専攻
教授　本多 正平（ほんだ しょうへい）
E-mail：shonda[at]m.tohoku.ac.jp
＊[at]を@に置き換えてください

Posted on：2022年1月24日