発表のポイント

● 数式を使ったモデルで経済の様々な課題を表現し、解析する数理経済学等で利用される因子分析モデル^注1の因子と平均相関係数との数学的関係を明らかにしました。因子分析モデルの重要な因子の決定に供され、同モデルの計算効率の向上が見込まれます。

● この知見は、金融時系列データ等の経済データの変動を統計的に説明したり、予測したりする際に有益です。また経済に限らず、電力のポートフォリオやワクチン設計の統計的方法の改善にも応用できると期待されます。

□ 東北大学ウェブサイト

概要

現代はデータサイエンスの時代であり、高次元のデータを高速・高精度で分析する手法の開発がますます重要になってきています。日経平均株価^注2などの金融時系列データは多種多様な事象から影響を受けており、経済政策や金融取引のために重要です。こうした株価などの複数の変数で構成されたデータを分析する数学的モデルの一つが因子分析モデルです。因子分析では少数の要因（因子）によって簡潔に説明でき、精度の高い経済政策や金融取引をタイミングよく実施することにつながります。

因子の特定に際しては、変数の間の相関係数を網羅的に算出して相関行列^注3を作成した上で、相関行列を効率よく説明するための「軸」（固有ベクトル）を計算します。固有ベクトルの計算は、取り扱う変数が増えれば増えるほど難しくなります。

東北大学大学院理学研究科数学専攻の赤間陽二准教授は、大規模高次元データから作られるサンプル相関行列の固有値^注4の極限分布^注5をランダム行列理論^注6により明示化しました。因子分析モデルにおいて、重要な因子、つまり、大きな固有値を持つ因子を容易に選択できるようになり、因子分析の速度の向上に資するものです。

因子分析は経済学のみならず、心理学、医学など実験や定量的な分析を重視する様々な分野でも利用されており、本研究が寄与する領域やトピックは広範に及ぶと期待されます。

本研究は2023年4月19日に経済理論の専門誌International Journal of Theoretical and Applied Financeに掲載されました。

詳細な説明

研究の背景

リスク管理と資産配分において、サンプル相関行列は重要です。サンプル相関行列は、ポートフォリオのリスク評価や資産配分の最適化に必要な情報を提供し、リスク分析や統計的分析にも役立つ、非常に重要な指標です。例えば、金融資産についての理論にポートフォリオ理論（Markowitz 1959、Eltonら2014）があります。その柱の一つは相関（または共分散）行列の研究です。平均収益とリスクを持つ一連の資産が与えられた場合、全体のポートフォリオが固定されたリスクレベルのために最良のリターンを提供する、あるいは、与えられた全体的なリターンに対して最小限のリスクを提供する、各金融資産の最適な重みを求めます。

これらの最適化では、共分散/相関行列の固有値から「信号」（リターンの急激な変化）を検出することが重要です。しかし、金融におけるサンプル共分散行列^注7やサンプル相関行列の固有値からランダムな固有値を排除するためのさまざまな方法が研究されてきました（参考文献1）。

なかでも、S&P500^注8（またはその他の主要市場）のN銘柄の株価のリターンの取引日数Tの時系列に関するサンプル相関行列Cを観察したところ、行列Cの固有値のヒストグラムが、指数T/NのMarcenko-Pastur（マルチェンコ-パスツール）分布の密度関数にほぼ当てはまることがわかっていました（参考文献2）。ただし、その密度関数の縮尺が、Cの最大固有値λをNで割った値を1から引いた数1−λ/Nになっていて、λに対応する固有ベクトルはN成分全てがほぼ等しくなっていました。Lalouxら（2000）は、あてはまったMarcenko-Pastur分布の密度関数の範囲を、サンプル相関行列Cのランダム固有値の区間と解釈し、それ以外の固有値を信号とみなしました。

このような、Marcenko-Pastur分布を用いるLalouxら（2000）のアイデアは、電力のポートフォリオや、ワクチン設計の統計的方法に影響を与えました（参考文献3）。それ以来、株価のリターンの時系列に関するサンプル相関行列に対するLalouxらの発見的手法を数学的に解明することが求められていました。

今回の取り組み

研究グループはLalouxら（2000）の観察が、等相関行列の最大固有値に対応する固有ベクトルが等成分であるという事実との類似性に着目しました。ここで、等相関行列とは対角成分が1でその他の成分が1未満の非負の数ρである、正方行列のことで、そのN個の固有値は大きい方から(N−1) ρ+1とN-1個の1−ρです。

そこで、母集団が、N次元正規分布で変数の間に一定 の正の相関係数ρを持つ母集団を等相関正規母集団と呼び、ρを等相関係数と呼び、このような母集団から形成されたサンプル相関行列Cの固有値の極限分布に関する赤間-Husnaqilati（2022）の公式と、Lalouxら（2000）の観察を比較しました。

命題（赤間-Husnaqilati（2022））。等相関係数0≤ρ<1を持つN次元正規母集団から形成されたサンプル相関行列Cを考えます。TとNの比が正の定数Qに収束するように無限大に行くとします。すると、サンプル相関行列Cの固有値分布は指数がQで縮尺が1−ρであるMarcenko-Pastur分布に収束します。

指数Qと縮尺1−ρは、それぞれ、Lalouxら（2000）が金融相関行列の固有値の分布にあてはめたMarcenko-Pastur分布の指数T/Nと縮尺1−λ/Nに対応することに着想を得ました。

赤間准教授はまず、サンプル相関行列の最大固有値λの、サンプル相関行列のサイズNに対する割合が、等相関係数ρに収束することを証明しました。

次に、等相関正規母集団は因子がちょうど一つである因子分析モデルであることに着目し、母集団を一般の因子分析モデルに拡張しました。因子分析モデルは、(Fama-French 1993, 2015)が数理経済学で株価のモデルなどに供されています。一般の因子分析モデルに対して等相関係数に対応する量を定義し、一般の因子分析モデルから生成されるサンプル相関行列の固有値の極限分布を明示的に与えました。これにより、Lalouxら（2000）のMarcenko-Pastur分布に関する発見的手法を、数学的に裏付けました。

また、特に、ρが正である場合、N次元等相関行列の最大固有値（N−1）ρ + 1と2番目に大きな固有値 1−ρの差はN に関していくらでも大きくなることから、サンプル分散行列の最大固有値が漸近的に正規分布に従うことを証明しました。

さらに、我々が着目したλ/Nの意味を調べるために、期間TにおけるS&P 500のN銘柄の株価の実データの等相関係数の時系列を計算しました。EngleとKellyが2012年に提案した動的な等相関モデル（dynamic equicorrelation）を利用しました。すると、どのセクター（業種）でもλ/Nが実データの相関係数の時系列より大きく、密接な関係があることが判明しました。

今後の展開

最大固有値を高速に計算するアルゴリズムが存在するために、平均相関係数の目安を約1万倍高速に計算できるようになりました。セクターごとの複数の企業の株価の平均相関係数のその目安を用いて、セクターごとの性格を浮き彫りにできます。

今後は、互いに多様な相関構造を持つデータ生成モデルに対して、ランダム行列理論を用いることにより、重要主成分の個数を決定するための規則の振る舞いを調べることができます。

本成果は早稲田大学で8月に開催される数理経済学と統計学に関する第6回国際会議EcoSta 2023の招待分科会の招待講演でも発表されます。

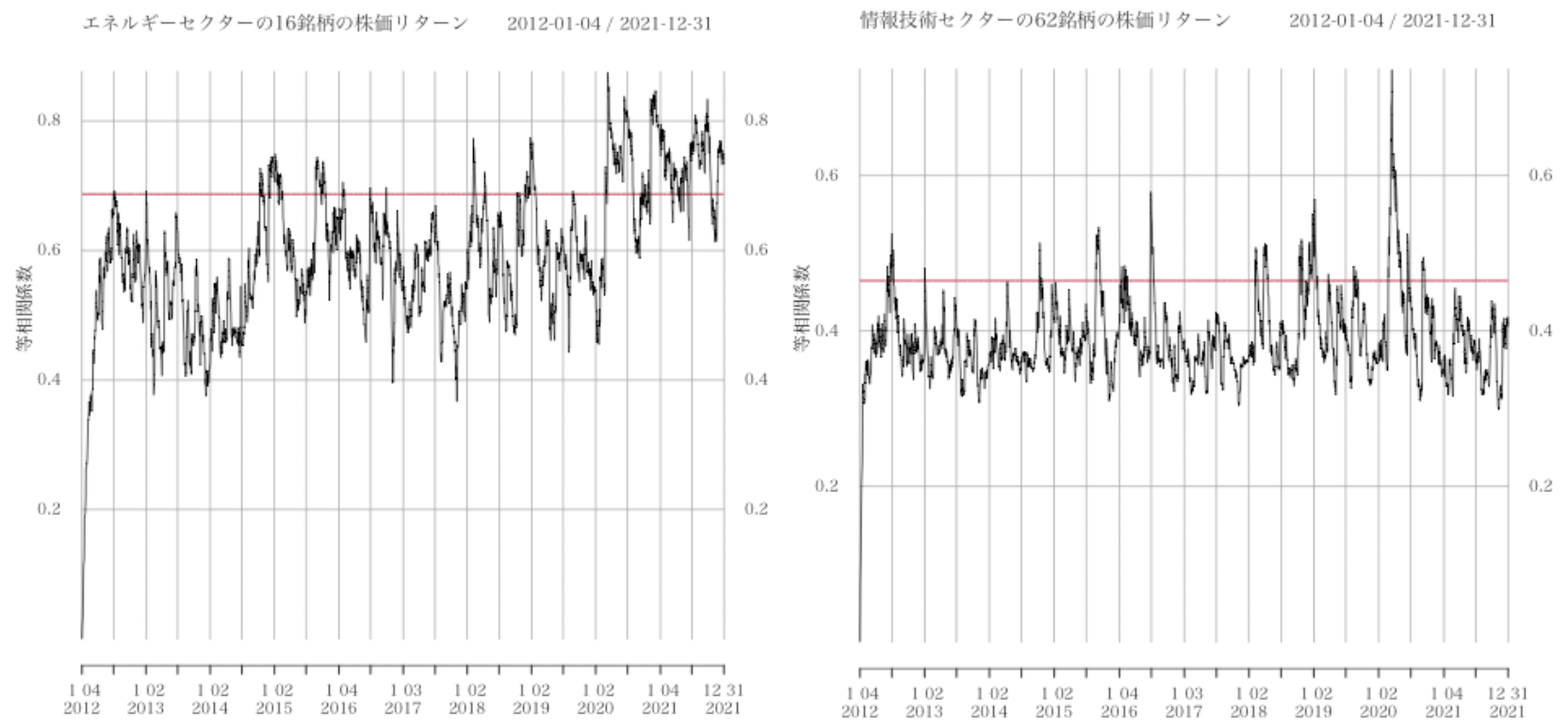
図1：左図は、2012/1/4-2021/12/31における、エネルギーセクターのS&P500の株価リターンの等相関係数の系列（黒）と、その期間の株価リターンの相関行列Cの最大固有値λを銘柄数Nで割った値（赤）。右図は、情報技術セクターの株価リターンに関する同様の図。

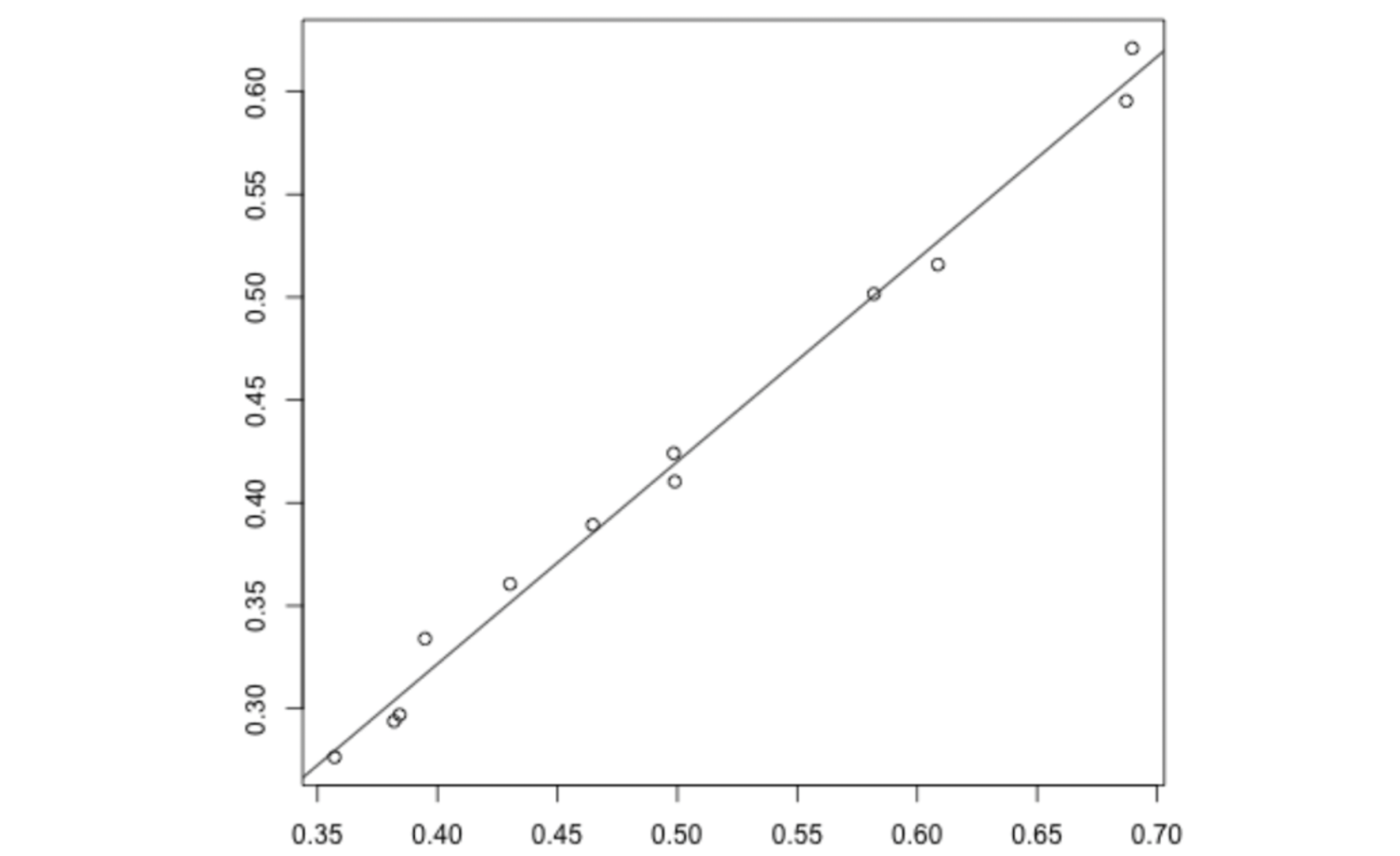
図2：S&P500のセクターごとの、株価リターンの相関係数の系列の時間平均(縦軸)と、λ/N (横軸)

用語説明

注1. 因子分析モデル：一連の変数の振る舞いを、より少数の基礎因子によって説明しようとする統計モデルのことです。因子分析モデルは、心理学をはじめ金融分野などで利用されます。金融分野において、金利や経済成長率、市場の変動などの少数の因子によって、ポートフォリオや資産のパフォーマンスを説明するためによく用いられます。

注2. 日経平均株価：日経平均、日経225とも呼ばれる日本の株式市場を代表する株価指数。各構成銘柄の株価に「株価換算係数」を乗じて「採用株価」とし、それらを合計したものを指数の連続性を維持するために調整された「除数」で割って求める。（https://www.nomura.co.jp/terms/Japan/ni/nk225.html）

注3. 相関行列：複数の変数間の相関係数を行列の形式でまとめたもので、統計学の分野で広く使われます。相関行列は、各変数のペア間の相関係数を表した正方形の行列で、対角線上には1が並びます。相関係数は、2つの変数間の線形関係の強さを表し、-1から1までの値をとります。相関係数が1に近い場合は、正の相関があり、二つの変数の一方が大きくなれば他方も大きくなるという傾向があります。

注4. 固有値：線形代数学において、正方行列がベクトルに作用する際に、そのベクトルをスカラー倍する数のことを指します。具体的に言うと、N次の正方行列Aに対して、ベクトルvがAv = λvを満たすとき、数λをvの固有値と呼びます。ここで、vは非ゼロベクトルで、AはN次の正方行列です。固有値は、行列の性質を表す重要な指標の一つです。

注5. 極限分布：サンプルの大きさと次元の比があらかじめ決まった定数に収束するように、両者を無限大にした極限における分布。

注6. ランダム行列理論：数学や物理学などの分野で用いられる、ランダムな行列の統計的な性質を研究する理論です。ランダム行列とは、行列の要素が確率的に選ばれる行列のことです。ランダム行列理論は、確率論、統計学、数学物理学などの分野で研究されており、多くの数学者や物理学者によって貢献がされています。

注7. 共分散行列：共分散行列とは、データの変数のペアの間の共分散を表す正方行列です。共分散とは、2つの変数の間の関係性を示す統計量であり、1つの変数が平均からどの程度ずれているかと同時に、もう1つの変数も平均からどの程度ずれているかを考慮します。

注8. S&P500：正式名称はStandard & Poor's 500 Stock Index（S&P500種株価指数）です。米国で時価総額の大きい主要500社が対象で、米国市場全体の相場の動きを表します。米指数算出会社のS&Pダウ・ジョーンズ・インディシーズが算出・公表しており、金融商品など幅広く活用されています。(https://www.nikkei.com/article/DGXZQOFM205ZZ0Q1A820C2000000/)

参考文献

参考文献1. Lalouxら（2000）、El Karoui（2008）、Ledoit-Wolf（2004、2012）、Ledoit-Péché（2011）、Donohoら（2018）
参考文献2. Lalouxら（2000）
参考文献3. 鶴見-所（2019）、Quadeerら（2018）

論文情報

タイトル：Correlation matrix of equi-correlated normal population: fluctuation of the largest eigenvalue, scaling of the bulk eigenvalues, and stock market
著者：赤間 陽二
*責任著者：東北大学大学院理学研究科 准教授 赤間 陽二
掲載誌：International Journal of Theoretical and Applied Finance
DOI：10.1142/S0219024923500061

問い合わせ先

＜研究に関すること＞
東北大学大学大学院理学研究科数学専攻
准教授 赤間 陽二（あかま ようじ）
E-mail: yoji.akama.e8@tohoku.ac.jp

＜報道に関すること＞
東北大学大学院理学研究科
広報・アウトリーチ支援室
TEL: 022-795-6708
E-mail: sci-pr[at]mail.sci.tohoku.ac.jp
*[at]を@に置き換えてください

Posted on：2023年5月 2日