発表のポイント

● 水が高いところから低いところへと流れるように、曲線に対して定まるある量が最も効率よく減るような曲線の挙動を数学的に追跡します。

● 与えられた紐で最も広い面積を囲むにはどうすればよいか？古代都市国家カルタゴの伝説にも関連する等周不等式について考えます。

● ある規則にしたがって時間とともに変形していく曲線の挙動を数学的に追跡することで見えてくるものとは？

概要

「長さが一定の単純閉曲線^（注１）の中で囲む面積が最大となる曲線はどのようなものか？」等周問題と呼ばれるこの問題は「ディドの問題」とも呼ばれます。それは、祖国を追われた王女が、漂流先の先住民との「牛一頭の皮で覆るだけの土地を与える」という約束のもと、牛の皮を細い紐状にして広大な土地を囲い、その土地の獲得が古代都市国家カルタゴの建国に繋がったと言われる伝説になぞらえたためです。等周問題の答えは円であり、その証明は既に様々に与えられていますが、本記事は、ある一般化された等周不等式の証明に関するものです。どのように一般化された問題なのかは以下で詳しく説明しますが、どのように証明するのか、ということに焦点を当てていきます。例えば、高いところから水を流すと水はより低いところへと流れていきます。つまり、一番低いところを探したいならば、高いところから水を流してみればよい、ということになります。特に、水は傾きが最も急に下がっている方向へと流れていくでしょう。一般に、傾きが最も急な方向へと流れていく様子を最急降下流や勾配流と呼びます。本記事で紹介する方法は、曲線に対して定まるある量に対して、それが適当な意味で最も効率よく減少する様子を記述する勾配流を構成し、その勾配流で曲線を動かしていくことで、曲線が行き着く先として等周不等式を証明しよう、というものです。ここで、曲線に対するどんな量を考えるのか、どういった意味の勾配流を考えるのか、というところが重要であり、この研究の本質とも言えます。以下でその詳細をなるべくわかりやすく説明したいと思います。

詳細な説明

研究の背景

まず、等周不等式をもう少し具体的に説明しましょう。γ を閉曲線とし、その長さを L(γ)、囲む面積を A(γ) と表せば、等周不等式は

と書くことができます。ディドの問題としては長さ L(γ) を与えたときに面積 A(γ) が最大となる γ を求めよという問題と見るわけですが、面積 A(γ) を与えたときに長さ L(γ) が最小となる γ を求めよ、と見ることもできます。その答えは円であり、様々な証明法が今では知られています（実際、半径 r の円の周長と面積を求めてみると等周不等式の等号が成り立つことがわかります）。本記事で扱う等周不等式は、これを回転数という概念を使って一般化したものです。回転数とは、非常に大雑把なことを言えば、反時計回りに 1 回りしたら 1、時計回りに 1 回りしたら -1 と数えて決まる整数のことです。

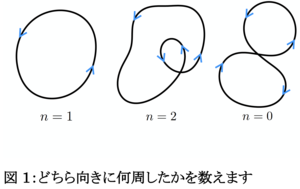例えば、反時計回りに向きを入れた円ならば回転数 1、８の字は 0、といった具合です（図1参照）。もともとの等周不等式は単純閉曲線（ 回転数は 1 ）を考えていたわけですが、回転数を含めた一般化として次のような等周不等式を考えてみましょう：

この n が曲線の回転数を表しているわけですが、n=1 の場合が古典的な等周不等式となりますので、回転数という概念を加えて一般化したと見ることができます。ちなみに、この一般化された等周不等式の等号が性質するならば、それは n 重巻きの円になります（円の周長と囲む面積は簡単に計算できますので、確かめてみてください）。この一般化した等周不等式を如何に証明するか（もちろん、既に幾つかの証明は知られています）が本記事の主題になりますが、それは次の節で説明することとして、まずは等周不等式の応用例を一つ紹介しましょう。

曲線の長さ L(γ) に対する勾配流の一つとして曲線拡散流というものがあります。曲線拡散流は、未解決な問題が多く残されており、今なお盛んに研究されている幾何学的発展方程式の一つです。近年、曲線拡散流は時刻無限大まで存在するか、存在するなら曲線の形状はどのようなものか、という問題について研究の進展が見られました。曲線拡散流は、曲線の長さ L(γ) を適当な意味で最も効率よく短くしていく一方で囲む面積 A(γ) を一定に保つ、という性質を持っています。この性質を見て、読者の皆さんも等周不等式が役に立つのではと感じたことと思います。実際、曲線拡散流によって閉曲線を変形していくとき、等周比 L(γ)²/4πA(γ) は単調に減少していきます。等周比の下限は 1 であり、等周比が 1 になるのは円だけですから、曲線拡散流によって変形される閉曲線は円になるのでは、と予想できることと思います。この予想が適当な仮定のもとで正しいことが2013年に証明されました( [4] )。

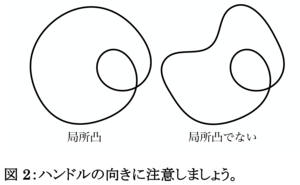論文 [4] の中では回転数 n が 1 でない場合は扱われていませんでした。その一つの要因は回転数に関して一般化した等周不等式が応用可能な形まで拡張されていなかったためです。当時は、閉曲線が、適当な回転対称性をもつことに加えて、局所的に凸ならば、一般化された等周不等式が成り立つ、ということしか証明されていませんでした。ここで、局所的に凸であるとは、その曲線に沿って車を反時計回りの向きに走らせるとき、ハンドルを常に左に切り続けていることに相当します（図２参照）。曲率の言葉で言うなら曲率が常に正ということです。曲線拡散流への応用を考えたとき、回転対称性の仮定は問題ないのですが、局所凸であるという仮定は大きな障害となります。曲線拡散流は高階の方程式であるがために、曲線が局所凸であることを保存するとは限らないからです。つまり、最初は一般化された等周不等式を適用できる閉曲線を考えていたとしても、曲線拡散流で変形しているうちに局所凸性が失われ、一般化された等周不等式を適用できなくなってしまうかもしれないということです。そこで、著者は局所凸性を取り除いて一般化された等周不等式を示す研究に取り組み、実際に証明することができました。 ( 論文 [1] として掲載されています。海外出張先で偶然一緒になった日本人研究者とこの話で盛り上がり、共同研究に至りました。) あわせて、論文 [1] において、その一般化された等周不等式を応用して、回転数が n である閉曲線を曲線拡散流で変形していくと時刻無限大で n 重巻きの円になることも合わせて証明しています。

今回の取り組み

さて、本題に戻りましょう。 n ≠ 0 は自然数とし、一般化された等周不等式を適当な勾配流を使って証明することを考えます。まずは、一般化された等周不等式を示す難しさの一つを説明したいと思います。

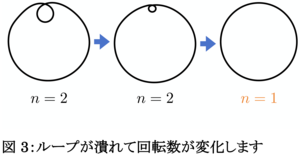円の内側に小さなループをつけた曲線を考えてみましょう。反時計回りに向きを入れておけば回転数は 2 ですから、示すべき等周不等式は n = 2 の場合となるはずです。しかし、内側のループをどんどん小さくして取り除き、ただの円にしてしまえば、その等周比は 1、つまり古典的な等周不等式になってしまいます（図３参照）。もともとは回転数が 1 より大きい曲線を考えていたとしても、変形の仮定で小さなループを取り除く操作をしてしまえば回転数をどんどん 1 に近づけていけるのです。これが一般化された等周不等式を示す際の一つの難しさと言えます。加えて、このループを潰すという操作が勾配流を用いた証明においても障害となり得ます。気軽に「ループを潰す」という話をしましたが、実際にループが潰れる瞬間には曲線は滑らかではなくなっています。実際、曲線の曲がり具合を表す幾何的量である曲率はループを潰した瞬間にはその点で発散しています。曲線に対する様々な勾配流が知られていますが、一般に曲率が発散するような「特異性」を許容できる勾配流はあまり知られていません。ほとんどの勾配流は曲率が発散するような強い特異性を許容できず、そこで止まってしまいます（数学的には、その時間発展方程式をそれ以上解き続けることができなくなる状態であり、それを一般に解の爆発、などと呼びます）。上記の考察のように、一般化された等周不等式を勾配流で示そうとすると、ループを潰すといった強い特異性が自然と発生することが予想されますので、使用する勾配流はその強い特異性を許容できる、もしくは発生させないものを選ばないといけない、ということになります。

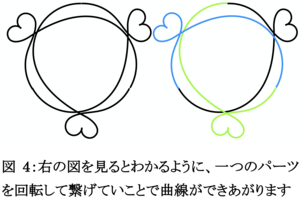勾配流を選択する上での注意について説明したところで、大切な仮定である回転対称性について説明しておきましょう。回転対称の度合いを表す自然数を m とし、回転数を表す n との間に 1 ≤ n ≤ m という仮定をします。回転数が n である m 次回転対称な曲線 γ の定義を式で表すことはもちろんできますが、ここでは例を見て理解してもらうことにしましょう。（図４参照。ただし、見やすいようにとハートをつけたため、n=-1、m=3 となり 1 ≤ n ≤ m を満たしていません。また、ハートのところに滑らかでない点があるので、そういった意味でもこのような曲線は本研究では考えていません。）つまり、一つのパーツを回転して組み立てた閉曲線ということです。論文 [1] で一般化された等周不等式を証明したときは、このパーツに関する等周不等式を証明し、それを回転対称性を用いて組み立てることで結論を得ていました。

さて、本記事の主題は勾配流を用いて等周不等式を示すことでした。どのような勾配流を選ぶかがアイデアの中心になります。我々は次のような量に注目しました：

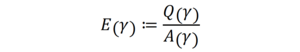
ここで、A(γ) は γ が囲む面積でしたが、Q(γ) は
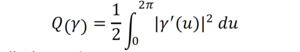と定義されるものです。曲線の長さ L(γ) は

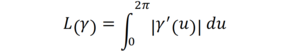
と与えられます^（注２）ので、Q(γ) では被積分関数を二乗していますから、もちろん Q(γ)は曲線の長さではありません。Q(γ) が L(γ)²/4 π なら E(γ) は等周比そのものですので、目的からして極めて自然な量に思えますが、これをあえて Q(γ) とするところが我々のアイデアでした。我々は、特異性を発生させない勾配流を構成することを念頭において、Sobolev 空間 H^{1 （注３）}の意味での勾配流を構成することを想定していました。その場合には Q(γ) という量は大変相性が良いのです。実際、E(γ) に対する H¹の意味での勾配流は時刻無限大で多重巻きの円（ただの円の場合も含む）に必ず収束することを証明できます。あとは、この勾配流を使って一般化された等周不等式をどう示すかなのですが、使うトリックは同じですので、等周不等式（ n=1 の場合）について説明しましょう。Q(γ) と L(γ) の指数の違いから一般に E(γ) は等周比以上になります。しかし、曲線を表示するパラメータとしてある特別なものを選ぶと、なんと E(γ) は等周比と等しくなってしまうのです。そこで、任意の初期曲線 γ₀ をその特別なパラメータで表示して、上で説明した勾配流で変形していくと次がわかります：

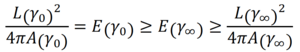
ここで、γ_∞ は、勾配流の収束先である、ある多重巻きの円です。その巻き数を k とすると、γ_∞ の等周比は k であることが簡単にわかります。面積 A(γ_∞ ) は正だとわかるので k は自然数、特に、k≥1 となります。これと上の不等式をあわせれば、どんな曲線を考えてもその等周比は 1 以上であるとなり、それは等周不等式に他なりません。回転数が一般の場合も同様の議論から証明できます( 論文 [3] )ので、読者の皆さんも考えてみてください。この証明方法は、証明方法自体が新しいということもあるのですが、論文 [1] で示した結果と比較すると、曲線の滑らかに課す仮定を少しだけ弱めることができる、という利点もあることを補足しておきたいと思います。

今後の展開

本記事で紹介したような、特異性を発生させない勾配流を曲線のような幾何的対象に対して構成しようとする研究がここ数年で注目を集めています（少なくとも著者の専門分野の近所では）。これまで一般的に考えられてきた勾配流との関係を調べたり、特異性が強い問題を解析することに応用したり、様々な方向の研究へと展開されていく可能性を秘めており、とても楽しみな題材であると著者は感じています。例えば、著者自身も曲線の曲げエネルギー^（注４）に対するこの類の勾配流を構成しており、これまで考えられてきた勾配流と比較すると、時刻無限大での収束を扱うときに余計な変換を施さなくても収束させることができる、という利点があることを証明しています( [2] )。

謝辞

本研究は JSPS 科研費 JP19H05599、JP19F19710、JP20KK0057、JP21H00990の助成を受けて行われています。

用語説明

注1：自己交差しない閉曲線のことです。ジョルダン閉曲線という呼び方もあります。
注2：今は曲線 γ を区間 0 ≤ u ≤ 2 π を動く変数 u を使ってパラメータ表示しているため、このように表現できます。
注3：一般に Sobolev 空間とは、弱い意味で定義される導関数が適当な可積分性をみたすような関数が構成する空間のことです。東北大学理学部数学科だと３年生後期に開講される「関数解析」を学ぶと、その詳細がもう少しわかるようになります。ここで用いた H¹ は、その関数とその関数の弱い意味の 1 階導関数がともに 2 乗可積分であるような関数から構成される空間のことです。
注4：曲線の曲がり具合を表す幾何的量である曲率を 2 乗して曲線に沿って積分することで定義されるものです。1600年代に提唱されて以降、今もなお研究の対象となり続けています。

論文情報

[1] T. Miura and S. Okabe, On the isoperimetric inequality and surface diffusion flow for multiply winding curves, Arch. Ration. Mech. Anal. 239 (2021), no. 2, 1111--1129.
[2] S. Okabe and P. Schrader, Convergence of Sobolev gradient trajectories to elastica, submitted, 2022.
[3] S. Okabe, P. Schrader, G. Wheeler, and V. Wheeler, A Sobolev gradient flow approach to the isoperimetric inequality, preprint, 2023.
[4] G. Wheeler, On the curve diffusion flow of closed plane curves, Ann. Mat. Pura Appl. (4), 192 (2013), no. 5, 931--950.

問い合わせ先

＜研究に関すること＞
東北大学大学院理学研究科数学専攻［web］
准教授　岡部真也（おかべしんや）
TEL: 022-795-7703
Email: shinya.okabe[at]tohoku.ac.jp
*[at]を@に置き換えてください

Posted on：2023年8月 7日