発表のポイント

● 宇宙最高の物質密度を誇る天体として中性子星がありますが、近年の観測によれば中性子星内部にクォーク^（注１）物質が存在すると予想されています。

● 近年の中性子星観測で示唆される「圧縮に伴う物質の激しい硬化」^（注２）をクォークに対するパウリ原理^（注３）、相対論的な運動エネルギーという基本的な2つの原理に基づき説明しました。

● 双対模型はこれまでのハドロンに関する物理学と中性子星内部の高密度物質に関する知見をつなぐ記述であり、様々な学際的展開が期待されます。

□ 東北大学ウェブサイト

概要

多数の原子核を含む系を圧縮していくと、多数の陽子・中性子を含む核物質になり、さらに圧縮すれば最終的にクォーク物質ができると予想されています。これらの超高密度物質は地上の実験室では実現不可能ですが、宇宙には中性子星という、わずか半径10kmの星に地球の30万倍の質量が詰まっている超高密度天体が存在します。 近年劇的に進展した中性子星観測によれば、従来の予想に反して、核物質からクォーク物質へと変化するにつれ物質が急激に『硬く』なっているようです。この謎を解くべく本研究では核物質からクォーク物質まで統一的に記述する理論を構築し、物質の急激な硬化の機構を説明しました。鍵となるのは、パウリの排他律という量子論的効果とクォークの相対論的運動です。前者はクォーク物質への変化を駆動し、それを通じてクォークの相対論的圧力が開放され、物質を硬くし、中性子星が重力崩壊するのを防ぐのです。

本研究で導入した理論は、今後予定されている重力波観測などの天体観測にとって重要なだけではなく、J-PARCで行われている原子核物理の実験に新しい動機を与えると期待されます。

本研究成果は2024年3月11日（米国東部時間）に米国物理学会が発行するPhysical Review Letters（電子版）に掲載されました。

詳細な説明

研究の背景

自然界で存在が確立している4つの基本的な力^（注４）のうち、「強い力」は原子核内部にある核子（陽子・中性子の総称）や核子を形作るクォークなどの運動を決める力となっています。その基礎理論である量子色力学（QCD）は、『色電荷』を持つクォークとグルーオンを素粒子として持つ理論で、基礎方程式は簡明ですが、そこから実に多彩な現象が導き出されます。その中でも特に重要なのは『カラーの閉じ込め』現象で、これは色電荷が特別な組み合わせを取る『白色』状態のみが観測可能であるという現象です。陽子や中性子などは3つの異なる色電荷を持つクォークが白色になるよう組み合わさった3体クォーク系（バリオン）です。また湯川博士のπ中間子^（注５）はクォークと反クォークが白色に組み合わさったクォーク2体系（メソン）です。これらを総称してハドロンと呼びます。核子は中間子を交換しながら相互作用を行ないますが、中間子はクォークからなるので、クォークは核子の構成要素でありつつ相互作用の担い手ともなっています。

ハドロン間の距離が十分離れているときにはクォークはハドロンの中に隠れており、系の状態はハドロン自由度を見ておけば説明できます。しかし大量の原子核を集めて圧縮していけば、まず沢山のバリオンからなるハドロン物質ができあがり、さらに圧縮すればバリオン内にあるクォークの自由度がやがて顕在化し、クォークを基本的自由度とするクォーク物質になると予想できます（図1）。このような極限状況下にあるQCDを調べる分野を「QCD物性」と呼びます。QCD物性の研究は、QCDが提唱された1970年代には本格的な研究が始まっており、「初期宇宙のクォーク・グルーオン・プラズマ」や「中性子星中心領域における高密度クォーク物質」など魅力的な話題が数多く提供され、現在もその研究対象は拡がり続けています。

近年の中性子星観測の急速な進展に伴い、低温・超高密度の物質の理解が深まっています。中性子星は半径10km程度の小さい星ですが、そこに太陽質量(M_◉)の1-2倍程度の質量が詰まっている超高密度な天体です。このような高密度物質は地上の実験室系では実現し得ません。質量と体積から大よその密度が見積もれますが、それはQCDの典型的なエネルギースケール程度になります。原子核物理の典型的な密度の単位としてよく標準核物質密度n0 = 0.16fm-3 (1fm=10-15m)^（注６）が用いられますが、中性子星の中心領域の密度は5n0程度にも達しており、これは核子同士が互いに重なり合うほどに高密度で、クォーク自由度が顕在化すると予想されます。

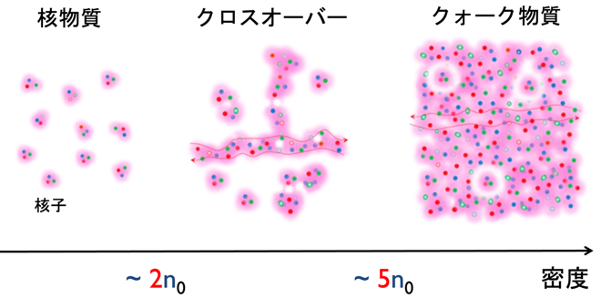
図1. バリオン密度を上げるにつれて原子核、核物質、クロスオーバー、クォーク物質へと変化していく様子。

太陽の半径は70万km程度ですから、中性子星内部には途方もないエネルギーが詰まっており、超強力な重力場^（注７）があることが想像できます（図2）。重力により中性子星内部にある物質は中心へと引っ張られますが、物質を圧縮すると圧力も上昇するので、重力と圧力上昇の力が釣り合うことで星の形状が保たれます。しかし、中心密度が大きくなり過ぎた場合、自身が作り出す重力を支えられなくなり、星は潰れてブラックホールになります。この議論から中性子星の質量には上限があることがわかりますが、この上限を決めるのは物質が持つエネルギー密度(ε)と圧力(P)を関係づける「状態方程式（EOS）」で、P(ε)と書きます。EOSが『硬い』というとき、考えているエネルギーにおける圧力が大きいことを意味します。　

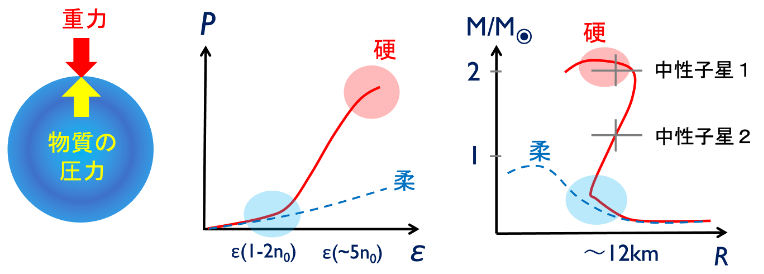
図2. 中性子星の状態方程式（圧力Pとエネルギーεの関係）と、それに対応して中性子星が取り得る質量(M)と半径(R)の関係。質量−半径曲線は、これまで観測された中性子星が持つ質量と半径を再現する必要があります。中性子星の構造は、中性子星内部のエネルギーが生み出す重力と、物質の圧力との釣り合いによって決定されます。エネルギーに比べ圧力が大きい場合、物質は硬い（圧縮しづらい）ので、中性子星のサイズは大きく、取り得る最大質量も大きくなります。ある質量以上では重力崩壊のため中性子星は実現せず、ブラックホールのみが存在可能です。

近年の観測により中性子星質量の上限は更新され続けており、2.1M_◉にも到達しています。つまり、中性子星内部はこれまで考えられていたよりもずっと硬いようなのです。一方、低密度領域においては、核子系に対する第一原理計算により制限がかかっており、それらは比較的柔らかいEOSを示唆しています。何故低密度で柔らかいEOSが高密度で急激に硬くなるのか、これを説明することは近年のQCD物性の中で最も重要な問題の一つです。これは物性物理の文脈でも前例がない新規な問題であり、かつ中性子星が関わる天体現象を理解するためにも大変重要な問題です。

以上に加えて、EOSの硬化の問題は、ハドロン物質とクォーク物質の関係を知るうえで重要です。長年ハドロン物質とクォーク物質は全くの別物と捉えられており、その移り変わりには気相・液相転移のような大きな変化（密度の飛びなど）を含む一次相転移が伴うと考えられていました。しかし一次相転移では、圧力は一定の下でエネルギー密度の不連続な上昇があるので、EOSは急激に柔らかくなってしまい、2.1M☉ を持つ中性子星の存在の説明が難しくなります。一次相転移を避けるべくクォーク物質の存在を否定する考え方もありますが、5n0程度の領域までハドロン自由度のみで話を閉じるのは不自然です。

近年、この困難を自然に避ける考え方として、「ハドロン物質とクォーク物質は滑らかなクロスオーバー転移で繋がっている」という考え方が徐々に浸透してきました。クォークは、低密度ではハドロン同士の相互作用の担い手として現れ、高密度へと向かうにつれ熱力学的における基本的自由度へと進化するのです。しかしクロスオーバー領域を具体的に記述しようとすると、基本的な自由度がハドロンかクォークなのかはっきりしないことによる困難に直面します。従って、ハドロン物質とクォーク物質に対する計算結果を、EOSのレベルで内挿するなどの現象論的手法が使われてきました。

今回の取り組み

ハドロン物質からクォーク物質へのクロスオーバー領域の物理を記述するべく、シアトルWashington大学の藤本悠輝研究員とLarry McLerran教授と協力して『クォーク・ハドロン双対模型』を構築しました。この模型はクォークに基づく記述とハドロンに基づく記述を対応付けることができ、一つの物理を二つの『言語』で記述することを可能にします。クロスオーバー領域のような自由度がはっきりしない領域でも二通りの記述ができるため、独立に議論されがちなハドロン的効果とクォーク的効果の関係を同時かつ多角的に追っていくことができます。

多体系の状態は一般にとても複雑なので、典型的かつ代表的な物理量に注目して系の状態を理解しようとする戦略がよく採用されます。双対模型では「主要な自由度がどの状態を占有しているか」を示す『状態占有率』の言葉で他粒子系の状態を特徴付けます。本研究では粒子の運動量^（注８）で状態を特徴付けます。状態占有率による記述は、特にバリオンやクォークのような同種のフェルミオンを多く含む系で有用です。量子論の基本的性質である『パウリの排他律』により、一つの状態を複数のフェルミオンが占有することはできませんが、これは「状態占有率は1を超えることはできない」という形で取り入れることができます。

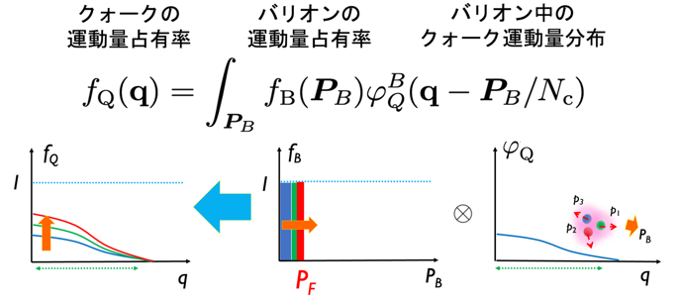
図3. 多体系における、クォークの運動量占有率、バリオンの運動量占有率、そしてバリオン単体中のクォーク運動量分布。各バリオンからの寄与を足し上げることでクォークの状態占有率が評価されます。

バリオンはクォーク3つからなる複合系ですから、バリオン内部にいるクォークが取る状態を指定すれば、バリオン状態占有率とクォーク状態占有率の間には関係がつきます（図3）。『ハイゼンベルグの不確定性原理』^（注９）により、バリオン中で狭い領域に閉じ込められたクォークは、低運動量から高運動量状態まで低い確率で占有しています。これら3つの占有率間の関係式が双対模型において最も重要な要素になります。関係式そのものは単純ですが、これをクロスオーバー領域に適用すると、後述するように大変非自明な結論が導かれます。

まず低密度領域を考えます。ここではバリオンの方が自然な自由度なので、バリオン占有率をインプットとして与えて、クォーク占有率をアウトプットとして出す、という見方になります。一方、密度が上がっていくとクォークの方が自然な自由度となりますから、クォーク占有率をインプットとして、バリオン占有率をアウトプットにしたいところです。この逆問題を解くのは一般的に難しいですが、バリオン中のクォーク分布の型として、この逆問題を簡単に解けるタイプのものが存在し、『可解模型』と呼びます。これは必ずしも現実を定量的なレベルで説明しませんが、模型の解析的計算や物理的概念のチェックを可能にするという意味でその重要性に疑いの余地はありません。本研究ではこのような可解模型を構築し、バリオン物質からクォーク物質までEOSの変化をバリオンとクォークの両方の言葉で記述しました。

バリオン・クォークの状態占有率の発展の仕方は以下の通り（図4）：

［1］低密度では、バリオン中のクォークは各状態を低い確率でしか占有しないため、バリオンの内部構造の詳細は問題とならず、バリオン状態はほぼ占有率１で低運動量から詰まっていきます。しかし密度を上げると、クォークの低運動量状態の占有率は急速に上昇します。この領域ではまだバリオンは重くて非相対論的なので、バリオンの数を増やすとエネルギー密度ばかり上昇し、一方で圧力はなかなか増えず、結果としてEOSは柔らかいものとなります。

［2］ある密度に到達すると、クォークの低運動量状態が完全に占有され、これ以上の密度ではバリオンのクォーク内部構造を無視できなくなります。これを『クォーク飽和』と呼ぶことにします。驚くべきことに、クォークの内部構造は通常バリオンが重なると考えられている密度の半分程度(2-3n0)で重要になります。これはバリオンが明確な表面を持った粒子ではなく、「クォークの染み出し」という量子的構造を持っていることによります。この飽和が起こる領域は、中性子星のEOSが急激に硬くなる領域とほぼ一致します。飽和後は、バリオン内部に閉じていたクォークの相対論的運動に伴う圧力が、系のEOSレベルで見え始めます。

［3］さらに密度を上げると、クォークの低運動量状態のかなりの部分が飽和する形でクォークの『フェルミ海』^{（注１０）}ができます。これは通常のクォーク物質の特徴づけに使われる概念です。一方、バリオン状態占有率に目を向けると、クォークのパウリ排他律を破らないようにするために、低運動量状態の占有率は低くならざるを得ず、高運動量状態でのみ通常の占有率を取ることが本研究の解析計算により示されました。これは結局パウリ排他律を避ける形でバリオンが相対論的になることを示しており、バリオンの言葉でもクォークの言葉でも相対論的圧力を記述できることを保証しています。

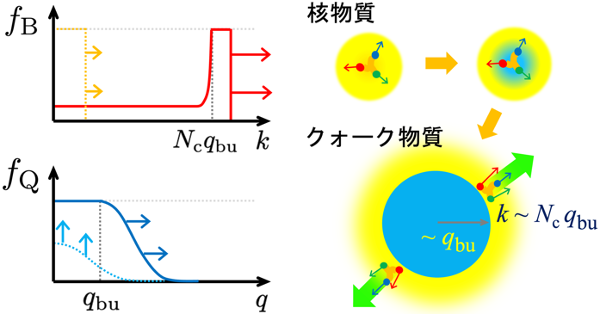
図4. 密度が上がったときのバリオンの状態占有率(fB)とクォークの状態占有率(fQ)の変化の様子。状態は粒子の持つ運動量（ここではバリオンはk,クォークはqと書いています）で特徴付けられています。点線は低密度の場合の運動量分布、実線は高密度の場合に対応します。バリオンの言葉では、低密度ではバリオンは低運動量状態を占有率1で占めていますが、高密度になると内部に含むクォークに対するパウリの排他律が効いて、バリオンは高運動量状態へと押し出されます（右図）。クォークの言葉では、低密度ではクォークの運動量は高運動量まで拡がりを持ち低運動量状態の占有率は小さいですが、高密度になると低運動量状態が飽和し、クォークのフェルミ海ができ、クォーク物質となります。

今後の展開

クォーク・ハドロン・クロスオーバーは、ハドロン物質からクォーク物質への転移を説明する有望なシナリオですが、ハドロンからクォークへの自由度の変遷を丁寧に追いかける必要があり、具体的な表現を与えるのは困難です。本研究で構築した双対模型は、その具体的表現の一つを状態占有率の言葉で与えています。模型が予言するクォーク飽和などの結論の多くは、パウリの排他律や相対論的運動エネルギーなどの基本的な性質で決まっており、模型の細かい詳細には依存しません。一方、どの密度でクォーク飽和が起こるか、それが相互作用や核子の構造の詳細にどう依るかはこれから明らかにされる問題です。今後は、バリオン間相互作用をクォークレベルで記述する研究やクォーク物質中でのハドロン相関を議論する研究が重要になっていくと考えられます。これらの物理は、ハドロン構造と相互作用に対する富岳を用いた格子QCDの大型数値シミュレーション^{（注１１）}、東海村で行われているJ-PARC実験^{（注１２）}などの大型プロジェクトなどと密接に関係します。双対模型はこれらの物理を繋ぐ有用な模型となると期待されます。

本研究ではアップ・ダウンクォークと呼ばれる２種類のクォークのみで解析しました。陽子・中性子からなる系を考える場合にはこれで十分なのですが、中性子星内部で2-3n0程度の高密度に到達すると、もう一種類のストレンジクォークと呼ばれるクォークも重要になると考えられています。バリオン側の言葉では、これはハイペロンと呼ばれる自由度に対応します。ハイペロンは核子より重く、系に登場する際に大きなエネルギー密度を持ち込みますが、一方で圧力の上昇には微々たる貢献しかしません。結果、EOSを柔らかくしてしまい２M◉を持つ中性子星の存在を説明できません。この問題は『ハイペロン・パズル』と呼び、天体・原子核物理の業界で大問題として知られています。核子とハイペロンの間に働く斥力を仮定することでハイペロンが出ないようにする記述がよく用いられますが、この記述の妥当性は（特に高密度では）定かではなく、より基礎的なクォークレベルでの記述が待たれています。双対模型はここでも重要な役割を果たすと考えられます。

　

謝辞

本研究は、宇宙創成物理学国際共同大学院（GP-PU）と以下の科学研究費補助金による助成のもとに進めてまいりました。

• 基盤研究（C）「高密度QCDの統一理論:ハドロン構造からクォーク物質まで」（JSPS KAKENHI Grants No. 23K03377）

• 新学術領域研究「第一原理から明らかにする階層構造の発現機構」（JSPS KAKENHI Grants No. 18H05407）

用語解説

注1.クォーク：クォークは、原子核や核子（陽子・中性子）は構成する素粒子であり、3種類の『色』電荷により区別されます。『白色』電荷を持つ複合クォーク粒子（ハドロン）のみが実験の最終状態として観測可能です。しかしハドロンが相互に重なり合うような超高密度物質においては、クォークが開放されクォーク物質を作ると考えられています。
注2.圧縮に伴う物質の激しい硬化：物質を圧縮すると内部のエネルギー密度と圧力の両方が大きくなります。硬い物質では、圧力の上昇の割合が大きく、なかなか圧縮できません。
注3.パウリ原理、またはパウリの排他律：素粒子はスピンと呼ばれる各々固有の角運動量を持っています。陽子・中性子、電子、クォークなどの粒子はスピン 1/2 を持ち、フェルミオンと呼ばれます。2 つの同種類のフェルミ粒子は同じ量子状態をとることができません。これをパウリの排他律と呼びます。
注4.自然界の4つの力：自然界においてその存在が確立している基本的な4つの力。重力、電磁力、弱い力、強い力から構成されています。
注5.π中間子：湯川秀樹博士により提唱された核子間に働く力を媒介する粒子で、ハドロンとしては最も軽い粒子となります。その軽い質量の起源は、南部陽一郎博士により『自発的対称性の破れ』の帰結として説明されました。
注6.標準核物質密度n0 = 0.16fm-3：原子核内の典型的な核子密度。1fm3という体積内に平均して0.16個の核子が見つかります（または適当に1fm3の体積を選んだとき、核子が一個見つかる確率が0.16)。高密度物質を考えるときの単位としてよく用いられます。
注7.重力場：エネルギーが高いと作り出される時空の歪み。例えば重い物質は質量＝エネルギーを持つので、周りの時空を歪めることで周りのものを引き付けます。歪んだ時空は光の進み方さえ曲げてしまいます。
注8.運動量：エネルギーの流れ。身近な例としては、p=mv など。ここでは mは粒子の質量（＝エネルギー)、vは粒子の持つ速度。
注9.ハイゼンベルグの不確定性原理：量子力学の特性を端的に表している原理。量子力学における粒子は、その位置(r)と運動量(p)を同時に正確に指定することができず、その不確定性の積であるΔpΔｒ は下限を持ちます。例えば狭い領域に閉じ込められた粒子は、幅広い運動量の値を取らざるを得ないので、高エネルギーの状態になります。
注10.フェルミ海：フェルミオンの運動量状態が、運動量ゼロからある一定の運動量状態まで占有されるような多体系の状態を表します。
注11.格子QCD数値シミュレーション：QCDの物理量を第一原理的に計算する方法。量子論では物理量を可能な状態を全て足し合わせることで観測量が計算されますが、可能な状態の数は膨大なので、状態の足し合わせを効率良く行なう必要があります。計算機の性能向上に伴い、様々な物理量が精度良く計算できるようになっています。一方、有限密度系では符号問題と呼ばれる大問題があり、第一原理計算はできていません。
注12.J-PARC実験：J-PARCは、茨城県東海村にある大強度陽子加速器施設であり、世界最高強度の陽子ビームとそこから二次生成されるハドロンビームを用いることで、非常に多彩な実験が可能です。素粒子、原子核の実験のみならず、物質科学・生命科学の実験も盛んに行われており、世界中の研究者が訪れます。

論文情報

タイトル：Momentum shell in quarkyonic matter from explicit duality: A dual model for cold, dense QCD
著者：Yuki Fujimoto, Toru Kojo, Larry McLerran
掲載誌：Physical Review Letters (Vol. 132, No. 11)
DOI：10.1103/PhysRevLett.132.112701

問い合わせ先

＜研究に関すること＞
東北大学大学院理学研究科物理学専攻
准教授　古城 徹（こじょう とおる）
TEL: 022-795-5582
Email: toru.kojo.b1[at]tohoku.ac.jp

＜報道に関すること＞
東北大学大学院理学研究科 広報・アウトリーチ支援室
電話：022-795-6708
Email：sci-pr[at]mail.sci.tohoku.ac.jp
*[at]を@に置き換えてください

Posted on：2024年4月10日