ポイント

● 素数の組み合わせ論が、高次元の世界でも成り立つことが明らかになってきています。

● 多様体の有理点のHasse原理（方程式の解を探す問題）や、Hilbertの第10問題（方程式の解の有無を判定するアルゴリズムの研究）に役立ちます。

● 韓国ドラマの制作スタッフを巻き込んだ人間ドラマも生まれました。

概要

素数が無限に存在することは、Euclidの著作『原論』（紀元前300年ごろ）に既に証明が載っています。p, p+2 がともに素数であるような p が無限個存在するという双子素数予想は、GoldbachやEuler （18世紀）は既に真剣に考察していたようですが、今日でも予想のままです。

Green-Taoの定理（2004年）は、素数からなるいくらでも長い等差数列が見つけられると述べています。これは例えば、p, p+d, ..., p+100d がすべて素数となるような p, d>0 が存在するということです。ただしこの性質を満たす具体的な p, d>0 はまだ見つかっていません。2024年までに見つかっている素数の等差数列の最長記録は27項のようです。
ともあれ、双子素数予想と比べて、動かせる変数 p, d が2つであることにより、現代の人類にも手が届く問題となっています。

以上のような、「素数の組み合わせ論」と呼ばれる研究を、「数体の素元」という高次元の設定で再構築する取り組みをしています。

詳細な説明

研究の背景

整数 d の平方根 √d や、虚数単位 i=√(-1) のような、代数的整数（だいすうてきせいすう）^（注1）と呼ばれる数たちが、現代代数学では通常の整数に並ぶ重要な地位を占めています。（円周率πや自然対数の底eは、どちらかというと解析学寄りの起源を持ち、代数的整数ではありません。）
代数的整数を有限個選んで、それをもとに加減乗除で作れる数をすべて集めると、数体（すうたい）と呼ばれる代数構造を得ます。代数的整数の選び方は無限にあるので、数体の種類も無限にあります。それぞれの数体（に含まれる代数的整数）の中には素元（そげん）と呼ばれる、素数の対応物があります。素数の組み合わせ論で考察されている諸問題の多くは、数体の素元という広い文脈で捉え直すことができます。

今回の取り組み

2019-2024年にわたる取り組みで、Green-Taoの定理と、それを深化したGreen-Tao-Zieglerの定理（文献 [GTZ], 2012年）という素数に関する定理を、数体の素元に対しても証明することができました。後者の結果は、私自身によって代数幾何の研究において、別の研究者によって整数論・数学基礎論（後述のHilbertの第10問題）の研究においても、すでに活用されています。

Green-Taoの定理の数体の素元への拡張は、東北大学の（元）同僚、関真一朗、見村万佐人、宗政昭弘、吉野聖人の各氏との共同研究で得られたものです（論文 [KMMSY]）。メンバーのひとりである関さんは、高校時代に韓国ドラマ（主人公が数学者を志します）を観て、劇中で印象的に使われたGreen-Taoの定理を、明確に意識するようになったとのことです。それがなければ今回の私たちの共同研究も始まらなかったかもしれません。

論文公開後、この経緯が当ドラマの数学顧問や脚本家の方々にも伝わりました。関さんとドラマ関係者は、互いに感謝の気持ちを伝え合うことができたそうです。不思議な巡り合わせに立ち会うことができ、私も感無量です。関さんの著書『グリーン・タオの定理』あとがきに詳しいことが書かれています。韓国の一般向け科学雑誌『数学東亜』でもこのエピソードが取り上げられました（文献 [東亜]）。

数体の中の代数的整数は、高次元の空間に等間隔に一様に散らばった点であり、素元はその中に一見ランダムに配置されています（図1）。Green-Taoの定理の数体版は、この素元の中に、どんな形（=有限個の点からなるパターン）でも見出すことができると述べています。まるで、夜空の星々をつないで星座を見出しているかのようです。そこで、私たちはこれを「数体の素元星座定理」と呼ぶことにしています。

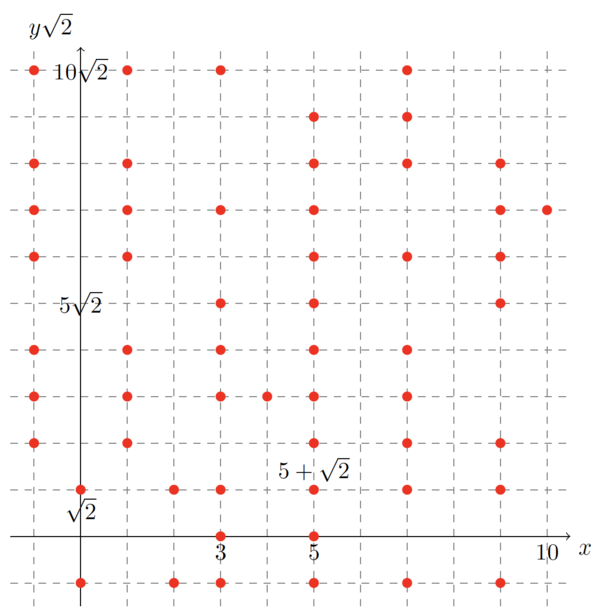
図1：集合 { x+y√2 | x,y は整数} の中の素元

「数体の素元星座定理」のあと、更に多様な素元のパターンを見出せるよう深化した、数体版Green-Tao-Zieglerの定理も証明することができました(論文 [K])。Green-Taoの定理（の一例）は、2つの変数 x, y の値を適切に選ぶと、有限個の1次式

x, x+y, ..., x+100y

の値が同時に素数になると述べています。（数体版）Green-Tao-Zieglerの定理では、y の係数だけでなく、x の係数や、定数項も変化させることが許されます。

今後の展望

多様な状況に適用可能な数体版Green-Tao-Zieglerの定理は、他分野への応用が期待されています。

たとえば、本家Green-Tao-Zieglerの定理を用いて有理数の世界でのみ証明できていた代数幾何の定理がある（少しだけ専門用語を使うと、有理数係数の具体的な形の方程式で定義された図形が、有理点に関するHasse原理を満たすという定理です）のですが、私の結果を用いることで、同定理がどんな数体を係数としても成り立つことが確認できました。

更に、私の予想だにしなかったことですが、数体版Green-Tao-Zieglerの定理を用いて、Hilbertの第10問題の否定的解決を、大幅に拡張することができたとの報が入りました（文献 [KP]）。
Hilbertの第10問題とは、1900年にHilbertが、20世紀の数学の指針として挙げた23問題のひとつです。整数係数の多項式方程式が任意に与えられるとき（たとえばFermatが考察した xⁿ+yⁿ=zⁿ）、これに整数解があるか否かを判定できるようなアルゴリズムを構築するよう求めています。1970年に、すべての多項式方程式に対応可能な単一のアルゴリズムは存在しないことが証明されました（否定的解決、図2）。

図2：Hilbertの第10問題の否定的解決

今回は、代数学研究者ならば当然、次に気になる、係数として整数だけでなく、数体の中の代数的整数（じつはもっと大幅に一般に、Z上有限生成な無限環（かん）^（注2））を考えた場合も、アルゴリズムの非存在が示せたそうです。
証明には楕円曲線の高度な理論を駆使します（アルゴリズムの存否に楕円曲線が関係あるのは一見すると不思議ですが、20年来知られ、使われてきた戦略です）。ある特定の性質を持つ楕円曲線を構成するために、定義方程式の係数をうまく選ぶ必要があり、私の結果が活用されています。

さらに他分野の研究に役立つ新たな素元の組み合わせ論的定理を証明する可能性を探り、有効な応用例の発見に向けて研究を深めていきたいと考えています。

謝辞

ここに記した研究を遂行する間、科研費JP18K13382およびJP22K13886の支援を受けました。また、日本学術振興会海外特別研究員としてミラノ大学（イタリア）に長期滞在する機会に恵まれました。ミラノでは公私にわたり多くの方々にお世話になり円滑に研究を進めることができました。

用語説明

注1. 代数的整数（だいすうてきせいすう）：代数的整数の正確な定義を述べておきます。複素数zが代数的整数であるとは、正整数 n≧1 と整数 a₁, ..., a_n を適切にとると、関係式 zⁿ + a₁ z^n-1 + ... + a_n =0 が成り立つことです。本文で述べた例は d を整数として z=√d でしたが（虚数単位は d=-1 の場合です）、この場合は実際に関係式 z^2 - d =0 が成り立っています。
注2. 環（かん）：四則演算のうち割り算を除いた演算が可能な集合を指します。たとえば全ての整数の集まりを考えると、整数同士の和・差や積が定義されていて、いつでも整数になります。なので整数全体のなす集合は、通常の和・差・積に関して環をなします。
「0で割る」以外の割り算が可能であるような環のことを、体（たい）といいます。有理数全体の集合は体をなします。「数体（すうたい）」という用語における「体」は、この意味です。
環がZ上有限生成であるとは、その環の元を有限個うまくとると、それらの元に対する有限回の加・減・乗算の結果としてどんな元でも得られることを言います。

論文情報

[KMMSY]
タイトル：Constellations in prime elements of number fields
著者：Wataru Kai, Masato Mimura, Akihiro Munemasa, Shin-ichiro Seki, Kiyoto Yoshino
雑誌等：プレプリント (2020), https://arxiv.org/abs/2012.15669

[K]
タイトル：Linear patterns of prime elements in number fields
著者：Wataru Kai
雑誌等：プレプリント(2023), https://arxiv.org/abs/2306.16983

参考文献

[GTZ]
タイトル：An inverse theorem for the Gowers U^s+1[N]-norm
著者：Ben Green, Terence Tao, and Tamar Ziegler
雑誌等：Annals of Mathematics 176 (2012), 1231-1372, http://dx.doi.org/10.4007/annals.2012.176.2.11

[KP]
タイトル：Hilbert's tenth problem via additive combinatorics.
著者：Peter Koymans, Carlo Pagano
雑誌等：プレプリント(2024), https://arxiv.org/abs/2412.01768

[東亜]
記事名：『[People] 일본 수학자, K-드라마 보고 n차원 별자리 정리 풀었다고?』(『日本の数学者、Kドラマを見てn次元星座定理を解決？』) 雑誌等：수학동아 (数学東亜), 2023年2月号 https://m.dongascience.com/news.php?idx=58580

問い合わせ先

東北大学大学院理学研究科数学専攻[web]
助教　甲斐　亘（かい　わたる）
Email：kaiw[at]tohoku.ac.jp
*[at]を@に置き換えてください

Posted on：2025年1月23日